【机器学习】正则化——理论推导以及实现方式（Python版）

【正则化】

回顾上一篇博客，出现过拟合的原因，无非就是学习模型学习能力过强，额外学习了训练集自身的特性，导致预测模型能够很好的适应于训练集，但是其泛化能力太差。出现过拟合的常见情况主要有以下2个方面：

• 特征参数过多，而训练样本过少
• 数据中包含异常样本，没有进行数据清洗（数据集自身特征太过明显）

正则化，是专门解决过拟合的优化算法。上一篇文章中我们不难理解，出现过拟合就是假设预测函数中的高阶项引起的，例如预测模型为：
$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3+\theta_4x_4^4$
那么减小其中高阶项的参数（权重）或者将其参数置为零，那么预测函数便可以很好的拟合数据，并且具备很好的泛化能力。在具体的算法实现过程中，我们在代价函数（CostFunction）中为特征参数添加相应的惩罚，使相应的系数权重减小，如下式：
$\color{red}J(\theta)=\frac{1}{2m}\left[\sum_{i=1}^{m}\left(h_\theta(x^{(i)})-y^{(i)}\right)^2+\lambda \sum_{j=1}^{n}\theta_j^2\right]$
其中$m$表示样本数量，$j$表示特征参数数量，$\lambda$称为正则化参数。
$\lambda$正则化参数的取值也直接影响到最终的预测函数$h_\theta(x)$,如果：

• $\lambda$取值过大，则导致整体$\theta$参数过小，会出现欠拟合的情况；
• $\lambda$取值过小，又不能很好地达到缩小特征参数的效果

所以选取合适的 $\lambda$很重要。

【正则化线性回归】

正则化线性回归的代价函数为：
$J(\theta)=\frac{1}{2m}\left[\sum_{i=1}^{m}\left(h_\theta(x^{(i)})-y^{(i)}\right)^2+\lambda \sum_{j=1}^{n}\theta_j^2\right]$
对于梯度下降算法：
$Repeat \begin{cases} \theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^{m}\left(h_\theta(x^{(i)})-y^{(i)}\right)x_0^{(i)}\\ \theta_j:=\theta_j-\alpha\left[\frac{1}{m}\sum_{i=1}^{m}\left(h_\theta(x^{(i)})-y^{(i)}\right)x_j^{(i)}+\frac{\lambda}{m}\theta_j\right] \end{cases}$
进一步整理为：
$\color{red} Repeat \begin{cases} \theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}{m}\left(h_\theta(x^{(i)})-y^{(i)}\right)x_0^{(i)}\\ \theta_j:=\theta_j(1-\alpha\frac{\lambda}{m})-\alpha\frac{1}{m}\sum_{i=1}^{m}\left(h_\theta(x^{(i)})-y^{(i)}\right)x_j^{(i)} \end{cases}$
对于正规方程法：
$\color{red}\theta=\left(X^{T}X+\lambda \begin{bmatrix} 0& \\ & 1 \\ &&1\\&&&\ddots\\&&&&1\end{bmatrix} \right)^{-1}X^{T}y$
图中的矩阵尺寸为$(n+1)*(n+1)$

【正则化逻辑回归】

正则化逻辑回归的代价函数为：
$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}\left[ -y^{(i)}\log\left(h_\theta(x^{(i)})\right)-(1-y^{(i)})\log\left(1-h_\theta(x^{(i)})\right) \right]+\frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2$
梯度下降实现为：
$\color{red} Repeat \begin{cases} \theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^{m}\left(h_\theta(x^{(i)})-y^{(i)}\right)x_0^{(i)}\\ \theta_j:=\theta_j-\alpha\left[\frac{1}{m}\sum_{i=1}^{m}\left(h_\theta(x^{(i)})-y^{(i)}\right)x_j^{(i)}+\frac{\lambda}{m}\theta_j\right] \quad\quad \text{for j=1,2, ..., n} \end{cases}$
以吴恩达逻辑回归正则化的作业为例，具体代码如下：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import scipy.optimize as opt
from sklearn.metrics import classification_report
from sklearn import linear_model

def readData(path,rename):
   data = pd.read_csv(path,names=rename)
   return data


def plot_data():
   positive =data[data['Accepted'].isin([1])]
   negative =data[data['Accepted'].isin([0])]
   fig,ax =plt.subplots(figsize=(8,5))
   ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
   ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
   ax.legend()
   ax.set_xlabel('Test 1 Score')
   ax.set_ylabel('Test 2 Score')



#特征映射
def feature_mapping(x1, x2, power):
   data = {}
   for i in np.arange(power + 1):
       for p in np.arange(i + 1):
           data["f{}{}".format(i - p, p)] = np.power(x1, i - p) * np.power(x2, p)

#     data = {"f{}{}".format(i - p, p): np.power(x1, i - p) * np.power(x2, p)
#                 for i in np.arange(power + 1)
#                 for p in np.arange(i + 1)
#             }
   return pd.DataFrame(data)


def sigmoid(z):
   return 1 / (1 + np.exp(- z))

def cost(theta, X, Y):
   left = (-Y) * np.log(sigmoid(X @ theta))
   right = (1 - Y)*np.log(1 - sigmoid(X @ theta))
   return np.mean(left - right)


def costReg(theta, X, Y, l=1):
   # 不惩罚第一项
   _theta = theta[1: ]
   reg = (l / (2 * len(X))) *(_theta @ _theta)  # _theta@_theta == inner product
   
   return cost(theta, X, Y) + reg

def gradient(theta, X, Y):
   return (X.T @ (sigmoid(X @ theta) - Y))/len(X) 

def gradientReg(theta, X, Y, l=1):
   reg = (1 / len(X)) * theta
   reg[0] = 0  
   return gradient(theta, X, Y) + reg

def predict(theta, X):
   probability = sigmoid(X@theta)
   return [1 if x >= 0.5 else 0 for x in probability]

if __name__ =="__main__":
   data = readData('ex2data2.txt',['Test 1','Test 2','Accepted'])
   print(data.head())
   plot_data()
   
       
   x1 = data['Test 1'].as_matrix()
   x2 = data['Test 2'].as_matrix()
   
   
   
   data2 =feature_mapping(x1,x2,power=6)
   print(data2)
   
   X=data2.as_matrix()
   Y=data['Accepted'].as_matrix()
   theta =np.zeros(X.shape[1])
   print(X.shape,Y.shape,theta.shape)
   
   print(costReg(theta,X,Y,l=1))
   print(gradientReg(theta, X, Y, 1))
   
   result = opt.fmin_tnc(func=costReg, x0=theta, fprime=gradientReg, args=(X, Y, 2))
   print(result)
   
   
   model = linear_model.LogisticRegression(penalty='l2', C=1.0)
   model.fit(X, Y.ravel())
   print(model.score(X,Y))
   
   final_theta = result[0]
   predictions = predict(final_theta, X)
   correct = [1 if a==b else 0 for (a, b) in zip(predictions, Y)]
   accuracy = sum(correct) / len(correct)
   print(accuracy)
   print(classification_report(Y, predictions))
   
   x = np.linspace(-1, 1.5, 250)
   xx, yy = np.meshgrid(x, x)

   z = feature_mapping(xx.ravel(), yy.ravel(), 6).as_matrix()
   z = z @ final_theta
   z = z.reshape(xx.shape)

   plot_data()
   plt.contour(xx, yy, z, 0)
   plt.ylim(-.8, 1.2)
   

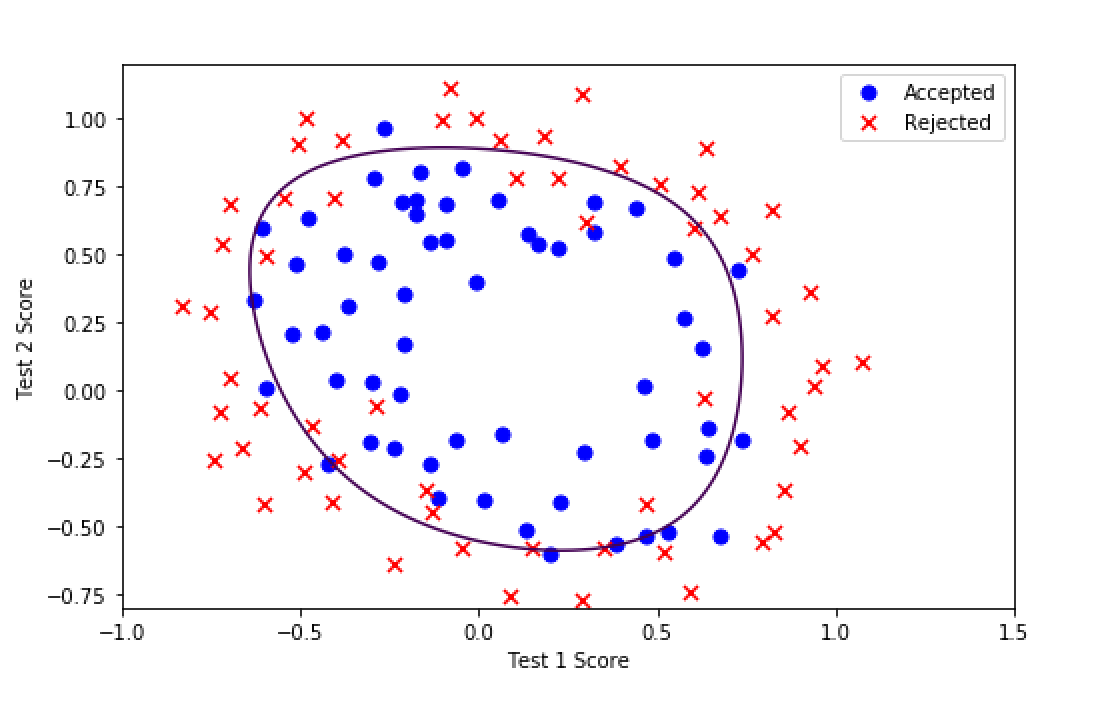
最终的决策边界图如下所示: