【朴素贝叶斯算法概述】
朴素贝叶斯算法是在贝叶斯公式的基础之上演化而来的分类算法,在机器学习中有着广泛的应用。朴素贝叶斯算法是条件化的贝叶斯算法,即在特征条件独立假说下的贝叶斯算法 。
【关于先验概率、后验概率的理解】
在进行理论推导之前,很有必要先普及一下什么是“先验概率 ”和“后验概率 ”,至少我在学习的过程中为区分此概念费了一番功夫。举例说明如下: 前验概率: 后验概率: 分析: c = { 男 , 女 } c=\{\text{男},\text{女}\} c = { 男 , 女 } x x x x ∈ X x\in X x ∈ X X X X 性别 ∈ { 长裤 , 裙子 } \text{性别} \in \{\text{长裤},\text{裙子}\} 性别 ∈ { 长裤 , 裙子 } P ( p a n t s ) = 6 0 ∗ 1 0 0 % + 4 0 % ∗ 5 0 % = 8 0 % P(pants) = 60*100\% + 40\%*50\% = 80\% P ( p a n t s ) = 6 0 ∗ 1 0 0 % + 4 0 % ∗ 5 0 % = 8 0 % P ( g i r l ∣ p a n t s ) = 穿长裤的女生/穿长裤的人 = P ( g i r l , p a n t s ) / P ( p a n t s ) = P ( g i r l ) ∗ P ( p a n t s ∣ g i r l ) / P ( p a n t s ) = 4 0 % ∗ 5 0 % ÷ 8 0 % = 2 5 % \begin{aligned}P(girl | pants) &= \text{穿长裤的女生/穿长裤的人}\\
&= P(girl, pants)/P(pants) \\
&= P(girl)*P(pants | girl) / P(pants) \\
&= 40\% * 50\%\div80 \% \\
&= 25\%
\end{aligned} P ( g i r l ∣ p a n t s ) = 穿长裤的女生 / 穿长裤的人 = P ( g i r l , p a n t s ) / P ( p a n t s ) = P ( g i r l ) ∗ P ( p a n t s ∣ g i r l ) / P ( p a n t s ) = 4 0 % ∗ 5 0 % ÷ 8 0 % = 2 5 % P ( c ∣ x ) = P ( x , c ) P ( x ) P(c|x)=\frac{P(x,c)}{P(x)} P ( c ∣ x ) = P ( x ) P ( x , c ) P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) → ( 后验公式 ) P(c|x)=\frac{P(c)P(x|c)}{P(x)} \rightarrow(\text{后验公式}) P ( c ∣ x ) = P ( x ) P ( c ) P ( x ∣ c ) → ( 后验公式 )
【贝叶斯决策论】
贝叶斯局策论,基于概率和误判损失来选择最优的类别标记。本部分内容将从以下问题出发:x x x N N N y = { c 1 , c 2 , ⋯ , c N } y=\{c_1,c_2,\cdots ,c_N\} y = { c 1 , c 2 , ⋯ , c N } λ i j \lambda_{ij} λ i j c j c_j c j c i c_i c i P ( c i ∣ x ) P(c_i|x) P ( c i ∣ x ) x x x c i c_i c i x x x R ( c i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) R(c_i|x)=\sum_{j=1}^{N}\lambda_{ij}P(c_j|x) R ( c i ∣ x ) = j = 1 ∑ N λ i j P ( c j ∣ x ) h : x → y h:x\rightarrow y h : x → y R ( h ) = E x [ R ( h ( x ) ∣ x ) ] R(h)=E_x[R(h(x)|x)] R ( h ) = E x [ R ( h ( x ) ∣ x ) ] x x x h ( x ) h(x) h ( x ) R ( h ( x ) ∣ x ) R(h(x)|x) R ( h ( x ) ∣ x ) R ( h ) R(h) R ( h ) R ( c ∣ x ) R(c|x) R ( c ∣ x ) h ∗ ( x ) = a r g m i n c ∈ y R ( c ∣ x ) h^*(x)=\underset{c \in y}{arg\ min}R(c|x) h ∗ ( x ) = c ∈ y a r g m i n R ( c ∣ x ) h ∗ h^* h ∗ R ( h ∗ ) R(h^*) R ( h ∗ ) 1 − R ( h ∗ ) 1-R(h^*) 1 − R ( h ∗ ) R ( c ∣ x ) R(c|x) R ( c ∣ x ) λ i j \lambda_{ij} λ i j λ i j = { 0 , i = j 1 , o t h e r w i s e \lambda_{ij}=\begin{cases}
0, & i =j \\
1 , & otherwise
\end{cases} λ i j = { 0 , 1 , i = j o t h e r w i s e R ( c ∣ x ) = 1 − P ( c ∣ x ) R(c|x)=1-P(c|x) R ( c ∣ x ) = 1 − P ( c ∣ x ) h ∗ ( x ) = a r g m a x c ∈ y P ( c ∣ x ) h^*(x)=\underset{c\in y}{arg \ max}P(c|x) h ∗ ( x ) = c ∈ y a r g m a x P ( c ∣ x ) x x x P ( c ∣ x ) P(c|x) P ( c ∣ x )
【贝叶斯模型的解释】
以上内容已经对问题解释的很清楚了,如果想要对样本进行分类,我们需要得到最大的P ( c ∣ x ) P(c|x) P ( c ∣ x ) P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) P(c|x)=\frac{P(c)P(x|c)}{P(x)} P ( c ∣ x ) = P ( x ) P ( c ) P ( x ∣ c ) P ( c ∣ x ) P(c|x) P ( c ∣ x ) P ( c ) P(c) P ( c ) P ( x ∣ c ) P(x|c) P ( x ∣ c ) x x x P ( x ) = x 的样本数 总样本数 P(x)=\frac{x\text{的样本数}}{\text{总样本数}} P ( x ) = 总样本数 x 的样本数 P ( c ∣ x ) P(c|x) P ( c ∣ x ) P ( x ∣ c ) P(x|c) P ( x ∣ c ) c c c P ( x ∣ c ) P(x|c) P ( x ∣ c )
【极大似然估计】
对于上式的计算,我们需要计算的内容主要为:P ( c ) 和 P ( x ∣ c ) P(c)\text{和}P(x|c) P ( c ) 和 P ( x ∣ c ) P ( c ) P(c) P ( c ) P ( x ∣ c ) P(x|c) P ( x ∣ c ) P ( x ∣ c ) P(x|c) P ( x ∣ c ) P ( x ∣ θ c ) P(x| \theta_c) P ( x ∣ θ c ) D c D_c D c D D D c c c θ c \theta_c θ c D c D_c D c P ( D c ∣ θ c ) = ∏ x ∈ D c P ( x ∣ θ c ) P(D_c|\theta_c)=\prod_{x\in D_c}P(x|\theta_c) P ( D c ∣ θ c ) = x ∈ D c ∏ P ( x ∣ θ c ) θ c \theta_c θ c P ( x ∣ θ c ) P(x| \theta_c) P ( x ∣ θ c ) θ c ^ \hat{\theta_c} θ c ^ L L ( θ c ) = log P ( D c ∣ θ c ) = ∑ x ∈ D c log P ( x ∣ θ c ) LL(\theta_c)=\log P(D_c|\theta_c)=\sum_{x\in D_c}\log P(x|\theta_c) L L ( θ c ) = log P ( D c ∣ θ c ) = x ∈ D c ∑ log P ( x ∣ θ c ) θ c \theta_c θ c θ c ^ \hat{\theta_c} θ c ^ θ c ^ = a r g m a x θ c L L ( θ c ) \hat{\theta_c}=\underset{\theta_c}{arg\ max}LL(\theta_c) θ c ^ = θ c a r g m a x L L ( θ c ) P ( x ∣ c ) ∽ N ( μ c , σ c 2 ) P(x|c)\backsim N(\mu_c,\sigma_c^2) P ( x ∣ c ) ∽ N ( μ c , σ c 2 ) μ c \mu_c μ c σ c 2 \sigma_c^2 σ c 2 μ c ^ = 1 ∣ D c ∣ ∑ x ∈ D c x \hat{\mu_c}=\frac{1}{|D_c|}\sum_{x \in D_c}x μ c ^ = ∣ D c ∣ 1 x ∈ D c ∑ x σ c ^ 2 = 1 ∣ D c ∣ ∑ x ∈ D c ( x − μ c ^ ) ( x − μ c ^ ) T \hat{\sigma_c}^2=\frac{1}{|D_c|}\sum_{x \in D_c}(x-\hat{\mu_c})(x-\hat{\mu_c})^T σ c ^ 2 = ∣ D c ∣ 1 x ∈ D c ∑ ( x − μ c ^ ) ( x − μ c ^ ) T
【朴素贝叶斯】
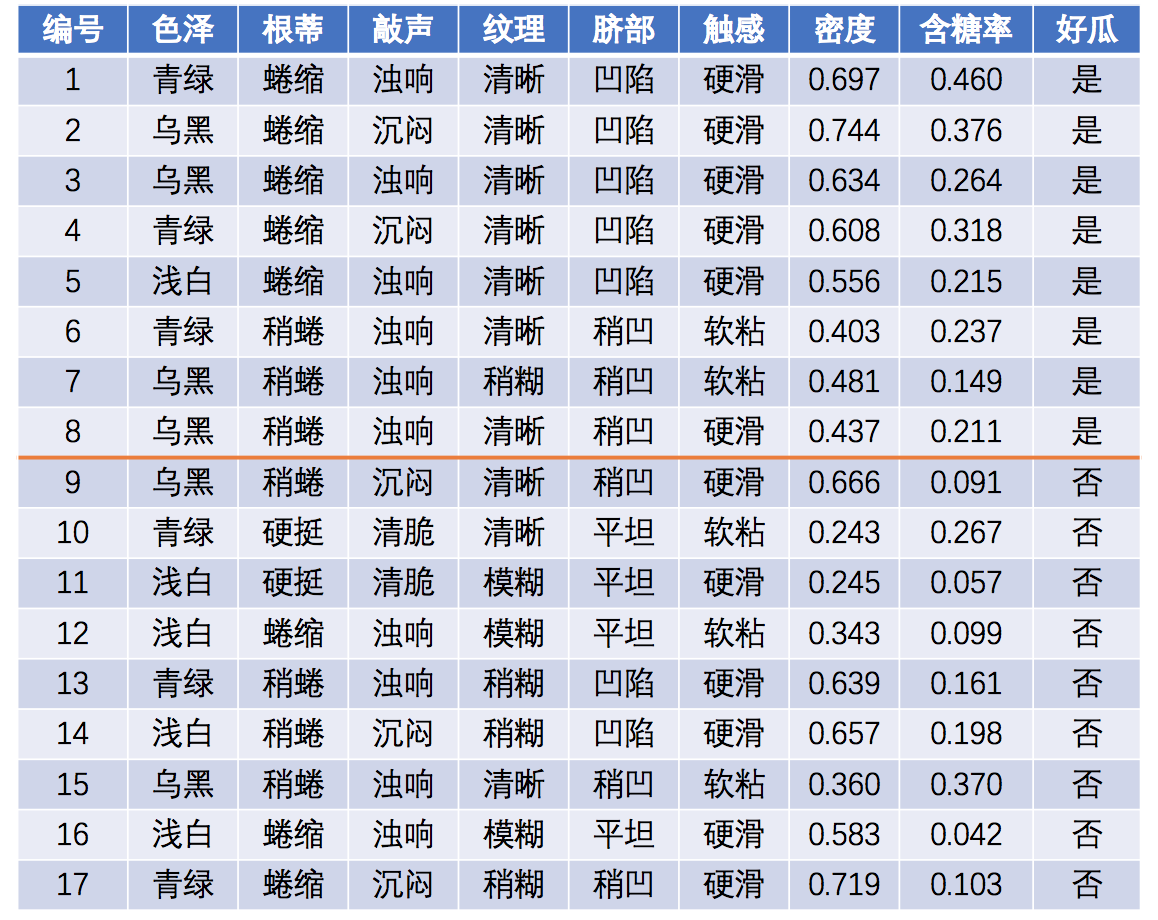
在此处引入全概率公式:P ( A ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P\left(A\right)=\sum_{i=1}^n{P\left(B_i\right)P\left(A|B_i\right)} P ( A ) = i = 1 ∑ n P ( B i ) P ( A ∣ B i ) 属性条件独立性假设,即所有属性相互独立 。可进一步将贝叶斯公式转化为:P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) = P ( c ) P ( x ) ∏ i = 1 d P ( x i ∣ c ) P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\prod_{i=1}^{d}P(x_i|c) P ( c ∣ x ) = P ( x ) P ( c ) P ( x ∣ c ) = P ( x ) P ( c ) i = 1 ∏ d P ( x i ∣ c ) d d d x i x_i x i x x x i i i P ( x ) P(x) P ( x ) h n b ( x ) = a r g m a x c ∈ y P ( c ) ∏ i = 1 d P ( x i ∣ c ) h_{nb}(x)=\underset{c \in y}{arg \ max}P(c)\prod_{i=1}^{d}P(x_i|c) h n b ( x ) = c ∈ y a r g m a x P ( c ) i = 1 ∏ d P ( x i ∣ c ) D c D_c D c D D D c c c P ( c ) P(c) P ( c ) P ( c ) = ∣ D c ∣ ∣ D ∣ P(c)=\frac{|D_c|}{|D|} P ( c ) = ∣ D ∣ ∣ D c ∣ D c , x i D_{c,x_i} D c , x i D c D_c D c i i i x i x_i x i P ( x i ∣ c ) P(x_i|c) P ( x i ∣ c ) P ( x i ∣ c ) = ∣ D c , x i ∣ ∣ D c ∣ P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|} P ( x i ∣ c ) = ∣ D c ∣ ∣ D c , x i ∣ p ( x i ∣ c ) ∽ N ( μ c , i , σ c , i 2 ) p(x_i|c)\backsim N(\mu_{c,i},\sigma_{c,i}^2) p ( x i ∣ c ) ∽ N ( μ c , i , σ c , i 2 ) μ c , i \mu_{c,i} μ c , i σ c , i 2 \sigma_{c,i}^2 σ c , i 2 c c c i i i p ( x i ∣ c ) = 1 2 π σ c , i exp ( − ( x i − μ c , i ) 2 2 σ c , i 2 ) p(x_i|c)=\frac{1}{\sqrt{2\pi}\sigma_{c,i}}\exp\left(-\frac{(x_i-\mu_{c,i})^2}{2\sigma_{c,i}^2}\right) p ( x i ∣ c ) = 2 π σ c , i 1 exp ( − 2 σ c , i 2 ( x i − μ c , i ) 2 ) 举例:
预测样本:P ( c ) P(c) P ( c ) P ( 好瓜=是 ) = 8 1 7 ≈ 0 . 4 7 1 P(\text{好瓜=是})=\frac{8}{17}\approx0.471 P ( 好瓜 = 是 ) = 1 7 8 ≈ 0 . 4 7 1 P ( 好瓜=否 ) = 9 1 7 ≈ 0 . 5 2 9 P(\text{好瓜=否})=\frac{9}{17}\approx0.529 P ( 好瓜 = 否 ) = 1 7 9 ≈ 0 . 5 2 9 P ( x i ∣ c ) P(x_i|c) P ( x i ∣ c ) P 青绿|是 = P ( 色泽=青绿|好瓜=是 ) = 3 8 = 0 . 3 7 5 P_\text{青绿|是}=P(\text{色泽=青绿|好瓜=是})=\frac{3}{8}=0.375 P 青绿 | 是 = P ( 色泽 = 青绿 | 好瓜 = 是 ) = 8 3 = 0 . 3 7 5 P 青绿|否 = P ( 色泽=青绿|好瓜=否 ) = 3 9 = 0 . 3 3 3 P_\text{青绿|否}=P(\text{色泽=青绿|好瓜=否})=\frac{3}{9}=0.333 P 青绿 | 否 = P ( 色泽 = 青绿 | 好瓜 = 否 ) = 9 3 = 0 . 3 3 3 P 蜷缩|是 = P ( 根蒂=蜷缩|好瓜=是 ) = 5 8 = 0 . 6 2 5 P_\text{蜷缩|是}=P(\text{根蒂=蜷缩|好瓜=是})=\frac{5}{8}=0.625 P 蜷缩 | 是 = P ( 根蒂 = 蜷缩 | 好瓜 = 是 ) = 8 5 = 0 . 6 2 5 P 蜷缩|否 = P ( 根蒂=蜷缩|好瓜=否 ) = 3 9 = 0 . 3 3 3 P_\text{蜷缩|否}=P(\text{根蒂=蜷缩|好瓜=否})=\frac{3}{9}=0.333 P 蜷缩 | 否 = P ( 根蒂 = 蜷缩 | 好瓜 = 否 ) = 9 3 = 0 . 3 3 3 P 浊响|是 = P ( 敲声=浊响|好瓜=是 ) = 6 8 = 0 . 7 5 0 P_\text{浊响|是}=P(\text{敲声=浊响|好瓜=是})=\frac{6}{8}=0.750 P 浊响 | 是 = P ( 敲声 = 浊响 | 好瓜 = 是 ) = 8 6 = 0 . 7 5 0 P 浊响|否 = P ( 敲声=浊响|好瓜=否 ) = 4 9 = 0 . 4 4 4 P_\text{浊响|否}=P(\text{敲声=浊响|好瓜=否})=\frac{4}{9}=0.444 P 浊响 | 否 = P ( 敲声 = 浊响 | 好瓜 = 否 ) = 9 4 = 0 . 4 4 4 P 清晰|是 = P ( 纹理=清晰|好瓜=是 ) = 7 8 = 0 . 8 7 5 P_\text{清晰|是}=P(\text{纹理=清晰|好瓜=是})=\frac{7}{8}=0.875 P 清晰 | 是 = P ( 纹理 = 清晰 | 好瓜 = 是 ) = 8 7 = 0 . 8 7 5 P 清晰|否 = P ( 纹理=清晰|好瓜=否 ) = 2 9 = 0 . 2 2 2 P_\text{清晰|否}=P(\text{纹理=清晰|好瓜=否})=\frac{2}{9}=0.222 P 清晰 | 否 = P ( 纹理 = 清晰 | 好瓜 = 否 ) = 9 2 = 0 . 2 2 2 P 凹陷|是 = P ( 脐部=凹陷|好瓜=是 ) = 6 8 = 0 . 7 5 0 P_\text{凹陷|是}=P(\text{脐部=凹陷|好瓜=是})=\frac{6}{8}=0.750 P 凹陷 | 是 = P ( 脐部 = 凹陷 | 好瓜 = 是 ) = 8 6 = 0 . 7 5 0 P 凹陷|否 = P ( 脐部=凹陷|好瓜=否 ) = 2 9 = 0 . 2 2 2 P_\text{凹陷|否}=P(\text{脐部=凹陷|好瓜=否})=\frac{2}{9}=0.222 P 凹陷 | 否 = P ( 脐部 = 凹陷 | 好瓜 = 否 ) = 9 2 = 0 . 2 2 2 P 硬滑|是 = P ( 触感=硬滑|好瓜=是 ) = 6 8 = 0 . 7 5 0 P_\text{硬滑|是}=P(\text{触感=硬滑|好瓜=是})=\frac{6}{8}=0.750 P 硬滑 | 是 = P ( 触感 = 硬滑 | 好瓜 = 是 ) = 8 6 = 0 . 7 5 0 P 硬滑|否 = P ( 触感=硬滑|好瓜=否 ) = 6 9 = 0 . 6 6 7 P_\text{硬滑|否}=P(\text{触感=硬滑|好瓜=否})=\frac{6}{9}=0.667 P 硬滑 | 否 = P ( 触感 = 硬滑 | 好瓜 = 否 ) = 9 6 = 0 . 6 6 7 p 密度:0.697|是 = p ( 密度=0.697|好瓜=是 ) = 1 2 π 0 . 1 2 9 exp ( − ( 0 . 6 9 7 − 0 . 5 7 4 ) 2 2 ⋅ 0 . 1 2 9 2 ) ≈ 1 . 9 5 9 p_{\text{密度:0.697|是}}=p(\text{密度=0.697|好瓜=是})=\frac{1}{\sqrt{2\pi}0.129}\exp\left(-\frac{(0.697-0.574)^2}{2\cdot 0.129^2}\right)\approx1.959 p 密度 :0.697| 是 = p ( 密度 =0.697| 好瓜 = 是 ) = 2 π 0 . 1 2 9 1 exp ( − 2 ⋅ 0 . 1 2 9 2 ( 0 . 6 9 7 − 0 . 5 7 4 ) 2 ) ≈ 1 . 9 5 9 p 密度:0.697|否 = p ( 密度=0.697|好瓜=否 ) = 1 2 π 0 . 1 9 5 exp ( − ( 0 . 6 9 7 − 0 . 4 9 6 ) 2 2 ⋅ 0 . 1 9 5 2 ) ≈ 1 . 2 0 3 p_{\text{密度:0.697|否}}=p(\text{密度=0.697|好瓜=否})=\frac{1}{\sqrt{2\pi}0.195}\exp\left(-\frac{(0.697-0.496)^2}{2\cdot 0.195^2}\right)\approx1.203 p 密度 :0.697| 否 = p ( 密度 =0.697| 好瓜 = 否 ) = 2 π 0 . 1 9 5 1 exp ( − 2 ⋅ 0 . 1 9 5 2 ( 0 . 6 9 7 − 0 . 4 9 6 ) 2 ) ≈ 1 . 2 0 3 p 含糖:0.460|是 = p ( 含糖率=0.460|好瓜=是 ) = 1 2 π 0 . 1 0 1 exp ( − ( 0 . 4 6 0 − 0 . 2 7 9 ) 2 2 ⋅ 0 . 1 0 1 2 ) ≈ 0 . 7 8 8 p_{\text{含糖:0.460|是}}=p(\text{含糖率=0.460|好瓜=是})=\frac{1}{\sqrt{2\pi}0.101}\exp\left(-\frac{(0.460-0.279)^2}{2\cdot 0.101^2}\right)\approx0.788 p 含糖 :0.460| 是 = p ( 含糖率 =0.460| 好瓜 = 是 ) = 2 π 0 . 1 0 1 1 exp ( − 2 ⋅ 0 . 1 0 1 2 ( 0 . 4 6 0 − 0 . 2 7 9 ) 2 ) ≈ 0 . 7 8 8 p 含糖:0.460|否 = p ( 含糖率=0.460|好瓜=否 ) = 1 2 π 0 . 1 0 8 exp ( − ( 0 . 4 6 0 − 0 . 1 5 4 ) 2 2 ⋅ 0 . 1 0 8 2 ) ≈ 0 . 0 6 6 p_{\text{含糖:0.460|否}}=p(\text{含糖率=0.460|好瓜=否})=\frac{1}{\sqrt{2\pi}0.108}\exp\left(-\frac{(0.460-0.154)^2}{2\cdot 0.108^2}\right)\approx0.066 p 含糖 :0.460| 否 = p ( 含糖率 =0.460| 好瓜 = 否 ) = 2 π 0 . 1 0 8 1 exp ( − 2 ⋅ 0 . 1 0 8 2 ( 0 . 4 6 0 − 0 . 1 5 4 ) 2 ) ≈ 0 . 0 6 6 P ( 好瓜=是 ) × P 青绿|是 × P 蜷缩|是 × P 浊响|是 × P 清晰|是 × P 凹陷|是 × P 硬滑|是 × p 密度:0.697|是 × p 含糖:0.460|是 ≈ 0 . 0 6 3 P(\text{好瓜=是})\times P_\text{青绿|是} \times P_\text{蜷缩|是}\times P_\text{浊响|是}\times P_\text{清晰|是}\times P_\text{凹陷|是}\times P_\text{硬滑|是}\times p_{\text{密度:0.697|是}}\times p_{\text{含糖:0.460|是}}\approx0.063 P ( 好瓜 = 是 ) × P 青绿 | 是 × P 蜷缩 | 是 × P 浊响 | 是 × P 清晰 | 是 × P 凹陷 | 是 × P 硬滑 | 是 × p 密度 :0.697| 是 × p 含糖 :0.460| 是 ≈ 0 . 0 6 3 P ( 好瓜=否 ) × P 青绿|否 × P 蜷缩|否 × P 浊响|否 × P 清晰|否 × P 凹陷|否 × P 硬滑|否 × p 密度:0.697|否 × p 含糖:0.460|否 ≈ 6 . 8 0 × 1 0 − 5 P(\text{好瓜=否})\times P_\text{青绿|否} \times P_\text{蜷缩|否}\times P_\text{浊响|否}\times P_\text{清晰|否}\times P_\text{凹陷|否}\times P_\text{硬滑|否}\times p_{\text{密度:0.697|否}}\times p_{\text{含糖:0.460|否}}\approx 6.80\times10^{-5} P ( 好瓜 = 否 ) × P 青绿 | 否 × P 蜷缩 | 否 × P 浊响 | 否 × P 清晰 | 否 × P 凹陷 | 否 × P 硬滑 | 否 × p 密度 :0.697| 否 × p 含糖 :0.460| 否 ≈ 6 . 8 0 × 1 0 − 5 0 . 0 6 3 > 6 . 8 0 × 1 0 − 5 0.063>6.80\times10^{-5} 0 . 0 6 3 > 6 . 8 0 × 1 0 − 5 P ( 清脆|是 ) = P ( 敲声=清脆|好瓜=是 ) = 0 8 = 0 P(\text{清脆|是})=P(\text{敲声=清脆|好瓜=是})=\frac{0}{8}=0 P ( 清脆 | 是 ) = P ( 敲声 = 清脆 | 好瓜 = 是 ) = 8 0 = 0
【拉普拉斯修正】
为了避免其他属性携带的信息被训练集中未出现的属性值“抹去”,在估计概率值时通常要进行“平滑”,常用“拉普拉斯修正”,令N N N D D D N i N_i N i i i i P ( c ) P(c) P ( c ) P ( x i ∣ c ) P(x_i|c) P ( x i ∣ c ) P ( c ) ^ = ∣ D c ∣ + 1 ∣ D ∣ + N \hat{P(c)}=\frac{|D_c|+1}{|D|+N} P ( c ) ^ = ∣ D ∣ + N ∣ D c ∣ + 1 P ( x i ∣ c ) ^ = ∣ D c , x i ∣ + 1 ∣ D c ∣ + N i \hat{P(x_i|c)}=\frac{|D_{c,x_i}|+1}{|D_c|+N_i} P ( x i ∣ c ) ^ = ∣ D c ∣ + N i ∣ D c , x i ∣ + 1
【案例代码】
import re, collections
def words ( text) : return re. findall( '[a-z]+' , text. lower( ) )
def train ( features) :
model = collections. defaultdict( lambda : 1 )
for f in features:
model[ f] += 1
return model
NWORDS = train( words( open ( 'big.txt' ) . read( ) ) )
alphabet = 'abcdefghijklmnopqrstuvwxyz'
def edits1 ( word) :
n = len ( word)
return set ( [ word[ 0 : i] + word[ i+ 1 : ] for i in range ( n) ] +
[ word[ 0 : i] + word[ i+ 1 ] + word[ i] + word[ i+ 2 : ] for i in range ( n-1 ) ] +
[ word[ 0 : i] + c+ word[ i+ 1 : ] for i in range ( n) for c in alphabet] +
[ word[ 0 : i] + c+ word[ i: ] for i in range ( n+ 1 ) for c in alphabet] )
def known_edits2 ( word) :
return set ( e2 for e1 in edits1( word) for e2 in edits1( e1) if e2 in NWORDS)
def known ( words) : return set ( w for w in words if w in NWORDS)
def correct ( word) :
candidates = known( [ word] ) or known( edits1( word) ) or known_edits2( word) or [ word]
return max ( candidates, key= lambda w: NWORDS[ w] )
correct( 'teal' )
输出结果:
【参考文献】