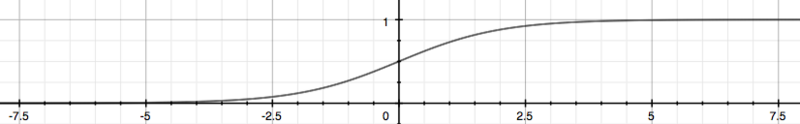分类问题

分类(classification)问题的一种实现方式是，使用线性回归(linear regression)，对于所有的预测结果，以某个值作为分界。比如小于0.5意味着0，大于0.5意味着1。然而，这种方法不够好，因为分类问题并不能用线性方程表示。

但分类问题依然是回归问题，只不过预测的结果限定在少量离散的结果集中。现在，我们把关注点集中在结果只有0和1的分类问题上，称为二值分类问题(binary classification problem)上。例如，如果我们要构建一个垃圾邮件分类器，

x(i)

可能是某封邮件的特征集，如果该邮件是垃圾邮件，那么对应的y为1，否则为0，因此y∈{0,1}。0有时也表示为负数符号-，1有时也表示为正数符号+。

y(i)

有时也叫训练集的标签(label)。

逻辑回归

假设函数

为了推导分类问题的假设函数。我们可以先忽略y其实是离散值这个事实，尝试使用线性回归模型来预测y。所不同的是，我们试图将y限制在如下范围：

0≤hθ(x)≤1

我们可以将之前的

θTx

嵌入到Logistic Function（下面公式中的g函数）：

hθ(x)=g(θTx)z=θTxg(z)=11+e−z

下图展示了这个sigmoid函数看起来的形态：

g(z)函数的值为(0,1)范围内的实数，这样比较容易适应分类问题。上述

hθ(x)

给出了结果为1的可能性。比如当

hθ(x)=0.7

时，意味着1的可能性是70%，而0的可能性是30%。我们用下面的公式来表达这个含义：

hθ(x)=P(y=1|x;θ)=1−P(y=0|x;θ)P(y=0|x;θ)+P(y=1|x;θ)=1

决策边界

观察上面公式，不难发现

θTx≥0y=1θTx<0y=0

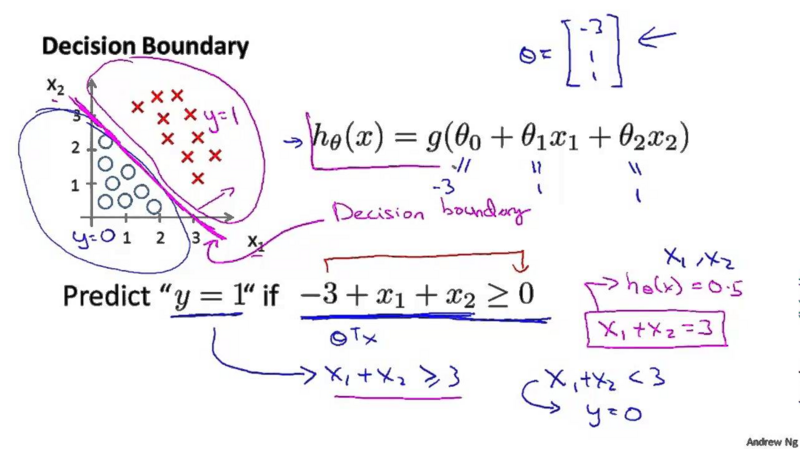
决策边界(decision boundary)是一条将y分割成两部分的线，一边是0，一边是1。决策边界由假设函数决定。

例如：

如上图，由

θ=−311

定义的

hθ(x)

将得到上图紫色的决策边界。

再比如：

观察上图的假设函数，不难发现这是个半径为1的圆形组成的决策边界，圆内部的

(x1,x2)

将使得y=0，反之，圆外部的

(x1,x2)

将使得y=1。

因此，假设函数形成了决策边界，不同的输入被假设函数落入不同的区域，从而得到分类的结果。所以，分类问题也是回归问题，只不过回归的结果是一组离散的值，并且我们采用上面的logistic函数来实现，因此，这种回归方法称为逻辑回归(logistic regression)。

代价函数

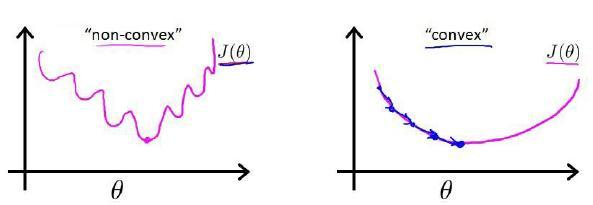
与线性回归一样，为了得到最优的假设函数，我需要先定义代价函数来衡量分类器的精度。但是我们不能直接使用线性回归中的代价函数，因为这会产生很多局部最优解，从而难以得到全局最优解，我们称这种函数为non-convex函数（convex这个术语在中文翻译中可能歧义，所以这里不做翻译）。下图展示了non-convex和convex的区别：

针对逻辑回归问题，定义如下convex的代价函数：

J(θ)=1m∑i=1mCost(hθ(x(i)),y(i))Cost(hθ(x),y)=−log(hθ(x)) ify=1Cost(hθ(x),y)=−log(1−hθ(x)) ify=0

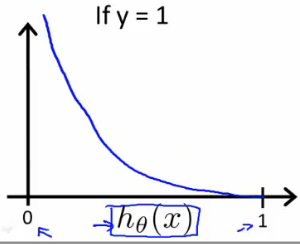
当y=1时，可以得到

hθ(x)

跟

J(θ)

的关系图：

上图的意思是，如果实际值是1，当

hθ(x)

的预测结果为1时，代价函数

J(θ)

为0；随着

hθ(x)

的预测结果趋近于0，

J(θ)

趋向于无穷大，即随着预测值越接近0，意味着代价越大。

当y=0时，可以得到

hθ(x)

跟

J(θ)

的关系图：

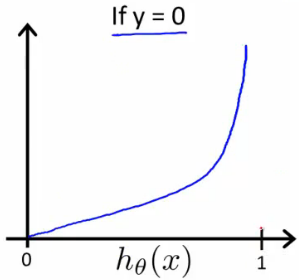
上图的意思是，如果实际值是0，当

hθ(x)

的预测结果为0时，代价函数

J(θ)

为0；随着

hθ(x)

的预测结果趋近于1，

J(θ)

趋向于无穷大，即随着预测值越接近1，意味着代价越大。

通过这样代价函数设计，我们可以保证代价函数是convex函数。

逻辑回归的梯度下降

上一节，我们定义了逻辑回归的代价函数，但是这个函数被分成了两部分：

J(θ)=1m∑i=1mCost(hθ(x(i)),y(i))Cost(hθ(x),y)=−log(hθ(x)) ify=1Cost(hθ(x),y)=−log(1−hθ(x)) ify=0

为了方便进行算法设计，需要将两部分合二为一：

J(θ)=−1m∑i=1m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]

观察上式，分别当y=0或者y=1时，函数的效果跟分开的时候一致。

对于逻辑回归依旧可以复用线性回归中的梯度下降算法来最小化J(θ)。

Repeat{θj:=θj−αm∑i=1m(hθ(x(i))−y(i))x(i)j}

只不过，在线性回归中上述公式的

hθ(x)

为：

hθ(x)=θTx

而在逻辑回归中上述公式的

hθ(x)

为：

hθ(x)=11+e−θTx

其他优化算法

共轭梯度法(Conjugate Gradient)，BFGS，L-BFGS算法可以用来代替梯度下降算法，因为这些算法在寻找最优θ的过程中往往更高效和精确。我们无需自己编写这些算法实现，而是直接使用现成的库，因为这些库在实现上已经做过高度优化和大量测试了。octave也支持这些算法。

在octave中，我们需要实现

J(θ)

和

∂∂θjJ(θ)

这两个计算公式，然后写一个类似下面的函数：

function [jVal, gradient] = costFunction(theta, X, y)   jVal = [...code to compute J(theta)...];   gradient = [...code to compute derivative of J(theta)...]; end

这个函数传入θ、输入数据集X、以及对应结果向量y，需要返回

J(θ)

以及用于迭代的

∂∂θjJ(θ)

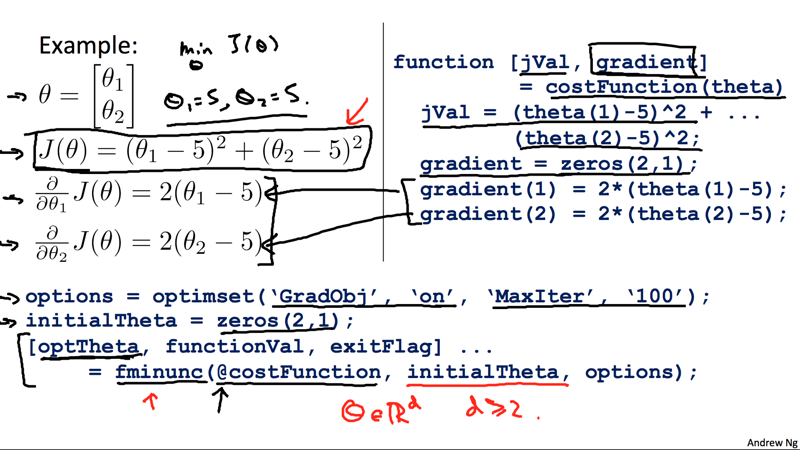
结果向量。然后使用fminunc函数，该函数会用更优化的算法来进行迭代，最终返回最优的结果：

options = optimset('GradObj', 'on', 'MaxIter', 100); initialTheta = zeros(2,1); [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

从中我们发现，在使用fminunc时，我们无需手动设定学习速率参数α。

下面是一个例子：

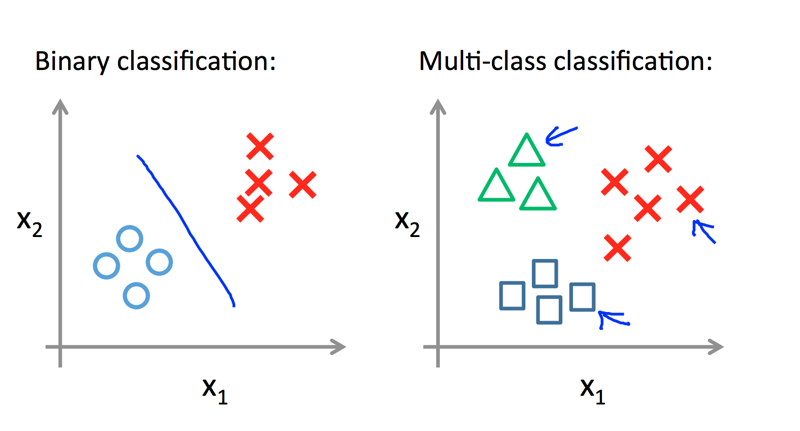
多级分类

上面我们讨论的分类问题最终的预测结果非0即1，也就是说，只有两种分类可能。在许多实际的问题中，分类结果有多种可能。例如：

• 将邮件分为工作、朋友、家庭等类

• 将天气分为晴天、阴天、雨天、下雪天

由于y={0,1...n}，我们可以把问题分割成n+1个二值分类问题，每个二值分类问题计算当前预测的y属于其中一个分类的概率。

例如，在第0个分类问题中，计算当前y属于第0类的概率

P(y=0|x;θ)

,那么y属于其他非0分类的概率为

1−P(y=0|x;θ)

。记

h(0)θ(x)=P(y=0|x;θ)

。以此类推，将每个二值分类问题都计算一遍，求出最大的概率，从而得到最终结果：

prediction=max(h(i)θ(x))

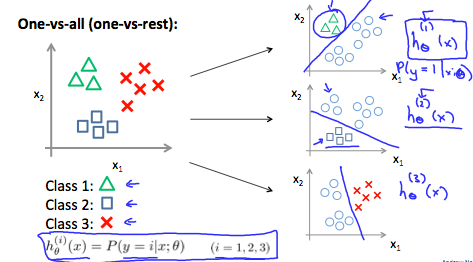
这种方式也叫One-vs-all，例如下面一个3级分类问题：

首先可以创建一个二值分类器，计算样本为三角形和非三角形的概率；然后创建一个二值分类器，计算样本为长方形和非长方形的概率；然后创建一个二值分类器，计算样本为叉和非叉的概率；最后将这三个分类其中概率最大的作为结果。每次我们考察其中一个分类，跟其他分类的概率，从而把多级问题转化为多个二值化分类器。

原文链接：https://segmentfault.com/a/1190000013818800