应如何重新调整 fft 点以获得与解析解相同的结果？

Question

我想使用 numpy fft 包进行快速傅立叶变换，然后我试图比较解析解和快速傅立叶变换之间的结果，虽然我可以看到我所做的曲线是相似的，很明显，尺度是不同的。我已经尝试了几种不同版本的频率（角频率、频率和波数），但我所有的尝试都没有奏效，并且在 numpy 文档中，不清楚快速傅立叶变换是如何准确定义的。例如，我想将时间指数函数的傅立叶变换转换为角频域，f(t)=Exp(-a|t|), F(w)=a/pi*(a²+w² )（此解析解有多个版本，具体取决于我们正在考虑的频率空间）def e(t):    return np.exp(-0.5*abs(t))def F(w):    return 0.5/(np.pi)*(1/(((0.5)**2)+((w)**2)))t=np.linspace(0,100,1000)w=np.fft.fftfreq(len(t))plt.plot(w,F(w),'o',label='F(w)')plt.legend()plt.show()fourier=np.fft.fft(e(t))plt.plot(w,fourier,'o')plt.show()我已经专门针对频率尝试了上述代码的多种不同变体，但我仍然没有达到 fft 和解析解相似的程度。有人可以帮我吗？

Answer 1

的傅立叶变换可以应用到积函数如np.exp(-0.5*abs(t))。但是离散傅立叶变换计算周期信号的傅立叶变换。请参阅https://dsp.stackexchange.com/questions/26884/about-fourier-transform-of-periodic-signal和FFTW 真正计算的内容。

因此，长度为 T 的帧的 DFT 对应于周期化帧的傅立叶变换。由于帧从 0 开始，因此计算了周期性右侧指数衰减的傅立叶变换： 如您所见，函数的一半未显示。让我们更正它并添加两侧指数衰减的周期增加部分。我使用频率作为参数：

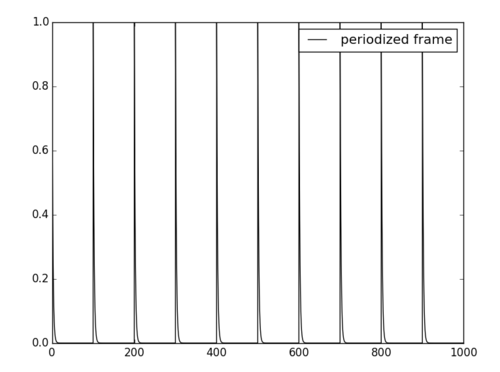
np.exp(-0.5*abs(t))

import matplotlib.pyplot as plt

import numpy as np

def e(t):

    return np.exp(-0.5*abs(t))

def F(w):

    return 0.5/(np.pi)*(1/(((0.5)**2)+((w)**2)))

def Fc(xi):

    #ok , that's sourced from https://en.wikipedia.org/wiki/Fourier_transform ... Square-integrable functions, one-dimensional, line 207

    return 2*0.5/(((0.5)**2)+(4*(np.pi*xi)**2))

framelength=100.

nbsample=1000

def ep(t):

    #the periodized negative part is added at the end of the frame.

    return np.maximum(np.exp(-0.5*abs(t)),np.exp(-0.5*abs(t-framelength)))

t=np.linspace(0,framelength,nbsample, endpoint=False)

#plotting the periodized signal, to see what's happening

ein=ep(t)

tp=np.linspace(0,10*framelength,10*nbsample, endpoint=False)

periodized=np.zeros(10*nbsample)

for i in range(10):

    for j in range(nbsample):

       periodized[i*nbsample+j]=ein[j]

plt.plot(tp,periodized,'k-',label='periodized frame')

plt.legend()

plt.show()

fourier=np.fft.fft(ep(t))/np.size(ep(t))*framelength

#comparing the mean is useful to check the overall scaling

print np.mean(ep(t))*framelength

print fourier[0]

print Fc(0)

#the frenquencies of the DFT of a frame of length T are 1/T, 2/T ... and negative for the second part of the array.

xi=np.fft.fftfreq(len(t), framelength/len(t))

# comparison between analytical Fourier transform and dft.

plt.plot(xi,Fc(xi),'o',label='F(xi)')

plt.plot(xi,np.real(fourier),'k-', lw=3, color='red', label='DTF')

plt.legend()

plt.show()

结果如下：

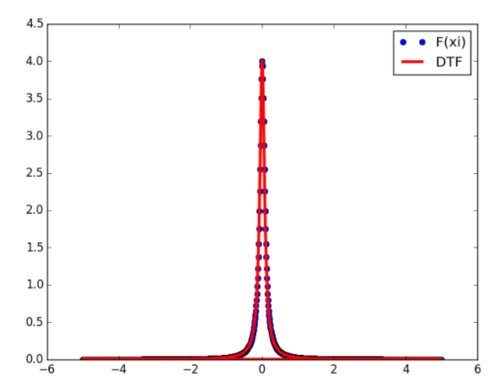
对于实验性非周期信号，当帧被周期化时会出现人为的不连续性。它会引起频谱泄漏，并应用窗口来衰减不连续性及其影响。其中一个潜在的窗口，称为泊松窗口，是一个两侧指数衰减！