为什么偶数 N 比奇数 N 花费更长的时间？

Question

我这里有一些代码可以在 python 中使用回溯来解决 n 个皇后问题。当我运行它时，赔率总是比偶数花费的时间少得多。当 n 达到 20+ 左右时，这一点尤其明显。有人知道为什么是这样吗？import timeglobal NN = int(input("Enter N: "))def display_solution(board):    print('\n'.join(['\t'.join([str(cell) for cell in row]) for row in     board]))def safe(board, row, col):    for i in range(col):        if board[row][i] == 1:            return False    for i, j in zip(range(row, -1, -1), range(col, -1, -1)):        if board[i][j] == 1:            return False    for i, j in zip(range(row, N, 1), range(col, -1, -1)):        if board[i][j] == 1:            return False    return Truedef solve_help(board, col):    if col >= N:        return True    for i in range(N):        if safe(board, i, col):            board[i][col] = 1            if solve_help(board, col + 1) is True:                return True            board[i][col] = 0    return Falsedef solve():    board = [[0 for x in range(N)] for y in range(N)]    if solve_help(board, 0) is False:        print("Solution does not exist")        return False    display_solution(board)    return Truestart = time.clock()solve()end = time.clock()print(N, "\t", end-start)我假设它必须与对角线的赔率与偶数不同有关。我也不确定这是否是所有回溯算法的问题，或者只是这个特定的代码。不管怎样，谢谢你的帮助。

Answer 1

当在第一列之一发生回溯并且必须尝试下一行时，该算法需要相当多的时间。将奇数 N 板与 N-1 板进行比较确实表明，偶数板的解决方案通常需要进行更多此类回溯/尝试下一个处理。例如，N=19 的解的左上角如下所示：

1 0 0 0 0

0 0 0 1 0

0 1 0 0 0

0 0 0 0 1*

0 0 1 0 0

0 0 0 0 0

0 0 0 0 0

0 0 0 0 0

前五列中的这 5 个皇后很快找到，因为它们是第一个不与之前的皇后发生碰撞的皇后。显然可以放置其他皇后而不必重新考虑前五个皇后。

对于 N=18，解决方案的同一角落如下所示：

1 0 0 0 0

0 0 0 1 0

0 1 0 0 0

0 0 0 0 0-

0 0 1 0 0

0 0 0 0 0

0 0 0 0 0

0 0 0 0 1*

注意标有减号的位置。这个看起来很有希望（就像 19 板一样）：它的调查需要相当长的时间才能得出无法正确放置其他皇后的结论。这种早期失败的代价。

因此，19 板的解决方案比 18 板更快地找到。

请注意，27 的解决方案比 26 的解决方案花费的时间略多，尽管这并不重要：看起来时间复杂度是O(2 n )，因此要比较不同板尺寸的时间，最好在对数 Y 轴：

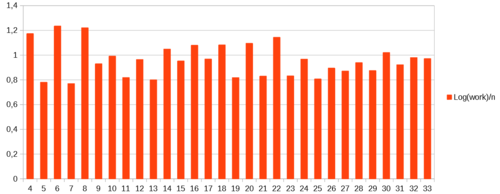
“work”表示函数safe执行的次数。

这种算法是否总是对偶数板花费相对更多的时间（与 N+1 板所需的时间相比）尚不清楚，但对于这几个板尺寸，它似乎与该算法自然形成的骑士跳跃有关，开始从左上角。请注意，这种模式如何完美地适用于 5 号和 7 号棋盘：下一个皇后可以坐在而不干扰先前定位的皇后的第一个位置始终是解决方案的一部分。而对于 4 号和 6 号棋盘，甚至没有任何解决方案在角落里有一个皇后，这是该算法的起点。

备择方案

从程序员的角度来看这个问题，有一种补救方法可以（平均而言）消除差异：以不同（甚至随机）的顺序选择列。事实证明，采用正常顺序是获得解决方案的效率较低的方法之一。

换档选择

该算法的一个简单转变，除非所有其他行都失败，否则您不考虑前两行，已经大大改变了统计数据：

在solve_help改变这个：

for i in range(N):

到：

for i in range(N):

   i = (i + 2) % N

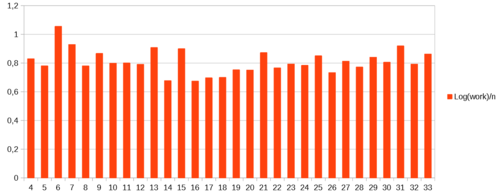
看看现在平均性能是如何提高的：log(work)/n的所有测量值都低于 1，除了 n=6。而且：现在更频繁地查看 N 的奇数值。

随机挑选

for i in random.sample(range(N), N):

以下是这样一次随机运行的结果：

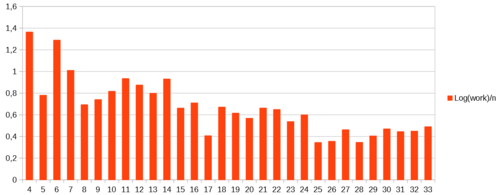
比原始订单更好的统计数据！当然，你会时不时地得到一个糟糕的统计数据，......因为它是随机的。但平均而言，它的表现（好得多）。

其他非随机顺序的方式可能包括col, 和N//2不同的系数, 如i = (i + col*2 + N//2) % N, ...等。但请参阅下面的最后评论。

其他备注

我将应用以下优化：跟踪哪些行、前向“对角线”和后向“对角线”已被采用。您可以为此使用列表或集合。请注意，如果两个单元格的坐标之和相等，则两个单元格位于同一对角线上。后对角线上的单元格的共同点是它们的坐标差相等。这样您就不必每次都在这些行中扫描“1”。

此外，board可能只是列号列表。无需存储所有这些零。仅保留用于显示。

最后，有一些简单的方法可以在线性时间内获得解决方案。参见维基百科。