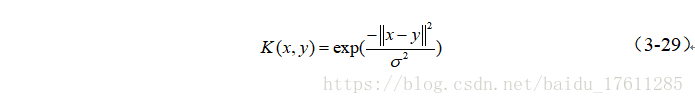异常检测-支持向量域描述算法及代码实现（Support Vector Domain Description）

以下是代码部分：

clc;
clear all;
close all;

%% 训练样本
% load('Iris.mat');       % Iris数据集每个数据由4维组成，一共3类，1:50,51:100,101:150，一行一个样本
% data = Iris(1:100,1:2); % 本次只取前2维的数据,以及2类进行分析
load('fn.mat');
% TrainX=PIread1';

data = f_n(1:418,:);% 轮廓主分量特征数据
TrainX = data;
%%%%%%%%
load('Iris.mat'); % 鸢尾花数据集
TrainX = Iris(51:100,:);
%%%%%%%%
%% 初始化二次规划数据，求得alf与支持向量个数
ker = struct('type','gauss','width',1.2);
nrx = size(TrainX,1);
labx=ones(nrx,1);
C=[0.09 1]; %0.8B

%% H
K=kernel(ker,TrainX,TrainX);
H = (labx*labx').*K; % 关键步骤，计算N*N的格莱姆矩阵

%% f
f = labx.*diag(H);

%% A & b 
A = -ones(1,nrx);
b = -1;

%% Been confirmed
Aeg = labx';
beq = 1.0;
lb = zeros(nrx,1);

%% ub
if length(C)>2
	ub = C;    
else
	ub = lb;
	ub(find(labx==1)) = C(1);
	ub(find(labx==-1)) = C(2);
end
% ub = ones(1600,1)/(nu*1600);

%% a0
rand('seed', sum(100*clock));
p = 0.5*rand(nrx,1); % 初值

[alf,fval,exitflag,output,lambda]= quadprog(2.0*H,-f,[],[],Aeg,beq,lb,ub,p); % 关键步骤，SVDD为凸优化问题，这里采用内点法求解

alf = labx.*alf;
epsilon = 1e-3;                    % 如果小于此值则认为是0
i_sv = find(((alf)>epsilon));        % 支持向量下标

% borderx = i_sv(find((alf(i_sv) < ub(i_sv))&(alf(i_sv) > epsilon)));


%% 计算R2值
n_sv = length(i_sv); % 支持向量个数
K1=kernel(ker,TrainX(i_sv,:),TrainX); 

tmp1 = 1;
tmp2 = -2*(sum((ones(length(i_sv),1)*alf').*K1,2));           % 行向量
tmp3 = sum(sum((alf*alf').*K),2);    
%% 计算R
R = 0;
for i=1:n_sv
    Ri = 1 - 2*K1(i,:)*alf + tmp3;
    R =  R + sqrt(Ri);
end;
R = R / n_sv;
R2 = R^2;

%% 
% load('fnnn');
load('dd_x');
hold on;
% plot(data(:,1),data(:,2),'+');
% plot(dd_x(:,1),dd_x(:,2),'.r');
% 
% idx_sv_boudary = find(alf>=C(1)-0.001); % 边界支持向量
% idx_sv_std = find(alf>epsilon & alf<C(1)-0.001);
% 
% % plot(data(i_sv,1),data(i_sv,2),'og','LineWidth',2);
% plot(data(idx_sv_std,1),data(idx_sv_std,2),'og','LineWidth',2);
% plot(data(idx_sv_boudary,1),data(idx_sv_boudary,2),'om','LineWidth',2);


f_n([760;4045;876;4196;3690;3455;1297;2304;3729;879;1600;3635],:) = [];
plot(f_n(:,1),f_n(:,2),'.',fnnn(:,1),fnnn(:,2),'xr');
hold on;
svddplot(i_sv,alf,TrainX,R2,ker.width,tmp3);
xlabel('λ1');ylabel('λ2');
title(' ');

以下是核函数格莱姆矩阵计算函数：

function [K] = kernel(ker,x,y)
% Calculate kernel function.   
%
% x: 输入样本,d×n1的矩阵,n1为样本个数,d为样本维数
% y: 输入样本,d×n2的矩阵,n2为样本个数,d为样本维数
%
% ker  核参数(结构体变量)
% the following fields:
%   type   - linear :  k(x,y) = x'*y
%            poly   :  k(x,y) = (x'*y+c)^d
%            gauss  :  k(x,y) = exp(-0.5*(norm(x-y)/s)^2)
%            tanh   :  k(x,y) = tanh(g*x'*y+c)
%   degree - Degree d of polynomial kernel (positive scalar).
%   offset - Offset c of polynomial and tanh kernel (scalar, negative for tanh).
%   width  - Width s of Gauss kernel (positive scalar).
%   gamma  - Slope g of the tanh kernel (positive scalar).
%
% ker = struct('type','linear');
% ker = struct('type','ploy','degree',d,'offset',c);
% ker = struct('type','gauss','width',s);
% ker = struct('type','tanh','gamma',g,'offset',c);
%
% K: 输出核参数,n1×n2的矩阵

%-------------------------------------------------------------%

switch ker.type
    case 'linear'
        K = x'*y;
    case 'ploy'
        d = ker.degree;
        c = ker.offset;
        K = (x'*y+c).^d;
    case 'gauss'
        
        s = ker.width;
        rows = size(x,1);
        cols = size(y,1);   
        tmp = zeros(rows,cols);
        for i = 1:rows
            for j = 1:cols
                tmp(i,j) = norm(x(i,:)-y(j,:));
            end
        end        
        K = exp(-0.5*(tmp/s).^2);

    case 'tanh'
        g = ker.gamma;
        c = ker.offset;
        K = tanh(g*x'*y+c);
    otherwise
        K = 0;
end

以下是绘制描述边界函数：

1. function [flags,R_p] = svddpredict(x,trainx,alf,R,ker,tmp3)  

2.     % x为测试样本m行d列，trainx为训练集n行d列  

3.     K1 = kernel(ker,trainx,x);  

4.     tmp2 = -2*(K1'*alf);  

5.       

6.     R_p = ones(size(tmp2))+tmp2+tmp3.*ones(size(tmp2));  

7.     flags = zeros(size(R_p));  

8.     index1 = find(R_p<=R);  

9.     index2 = find(R_p>R);  

10.     if length(index1>0)      

11.          flags(index1) = 1;  

12.     end;  

13.     if length(index2>0)  

14.          flags(index2) = -1;  

15.     end;  

16. end  

原文出处