-
0,Y,X1,X2,X3 1,5.1,3.5,1.4,0.2 2,4.9,3.0,1.4,0.2 3,4.7,3.2,1.3,0.2 4,4.6,3.1,1.5,0.2 5,5.0,3.6,1.4,0.2 6,5.4,3.9,1.7,0.4 7,4.6,3.4,1.4,0.3 8,5.0,3.4,1.5,0.2 9,4.4,2.9,1.4,0.2 10,4.9,3.1,1.5,0.1 11,5.4,3.7,1.5,0.2 12,4.8,3.4,1.6,0.2 13,4.8,3.0,1.4,0.1 14,4.3,3.0,1.1,0.1 15,5.8,4.0,1.2,0.2 16,5.7,4.4,1.5,0.4 17,5.4,3.9,1.3,0.4 18,5.1,3.5,1.4,0.3 19,5.7,3.8,1.7,0.3 20,5.1,3.8,1.5,0.3 21,5.4,3.4,1.7,0.2 22,5.1,3.7,1.5,0.4 23,4.6,3.6,1.0,0.2 24,5.1,3.3,1.7,0.5 25,4.8,3.4,1.9,0.2 26,5.0,3.0,1.6,0.2 27,5.0,3.4,1.6,0.4 28,5.2,3.5,1.5,0.2 29,5.2,3.4,1.4,0.2 30,4.7,3.2,1.6,0.2 31,4.8,3.1,1.6,0.2 32,5.4,3.4,1.5,0.4 33,5.2,4.1,1.5,0.1 34,5.5,4.2,1.4,0.2 35,4.9,3.1,1.5,0.1 36,5.0,3.2,1.2,0.2 37,5.5,3.5,1.3,0.2 38,4.9,3.1,1.5,0.1 39,4.4,3.0,1.3,0.2 40,5.1,3.4,1.5,0.2 41,5.0,3.5,1.3,0.3 42,4.5,2.3,1.3,0.3 43,4.4,3.2,1.3,0.2 44,5.0,3.5,1.6,0.6 45,5.1,3.8,1.9,0.4 46,4.8,3.0,1.4,0.3 47,5.1,3.8,1.6,0.2 48,4.6,3.2,1.4,0.2 49,5.3,3.7,1.5,0.2 50,5.0,3.3,1.4,0.2 51,7.0,3.2,4.7,1.4 52,6.4,3.2,4.5,1.5 53,6.9,3.1,4.9,1.5 54,5.5,2.3,4.0,1.3 55,6.5,2.8,4.6,1.5 56,5.7,2.8,4.5,1.3 57,6.3,3.3,4.7,1.6 58,4.9,2.4,3.3,1.0 59,6.6,2.9,4.6,1.3 60,5.2,2.7,3.9,1.4 61,5.0,2.0,3.5,1.0 62,5.9,3.0,4.2,1.5 63,6.0,2.2,4.0,1.0 64,6.1,2.9,4.7,1.4 65,5.6,2.9,3.6,1.3 66,6.7,3.1,4.4,1.4 67,5.6,3.0,4.5,1.5 68,5.8,2.7,4.1,1.0 69,6.2,2.2,4.5,1.5 70,5.6,2.5,3.9,1.1 71,5.9,3.2,4.8,1.8 72,6.1,2.8,4.0,1.3 73,6.3,2.5,4.9,1.5 74,6.1,2.8,4.7,1.2 75,6.4,2.9,4.3,1.3 76,6.6,3.0,4.4,1.4 77,6.8,2.8,4.8,1.4 78,6.7,3.0,5.0,1.7 79,6.0,2.9,4.5,1.5 80,5.7,2.6,3.5,1.0 81,5.5,2.4,3.8,1.1 82,5.5,2.4,3.7,1.0 83,5.8,2.7,3.9,1.2 84,6.0,2.7,5.1,1.6 85,5.4,3.0,4.5,1.5 86,6.0,3.4,4.5,1.6 87,6.7,3.1,4.7,1.5 88,6.3,2.3,4.4,1.3 89,5.6,3.0,4.1,1.3 90,5.5,2.5,4.0,1.3 91,5.5,2.6,4.4,1.2 92,6.1,3.0,4.6,1.4 93,5.8,2.6,4.0,1.2 94,5.0,2.3,3.3,1.0 95,5.6,2.7,4.2,1.3 96,5.7,3.0,4.2,1.2 97,5.7,2.9,4.2,1.3 98,6.2,2.9,4.3,1.3 99,5.1,2.5,3.0,1.1 100,5.7,2.8,4.1,1.3 101,6.3,3.3,6.0,2.5 102,5.8,2.7,5.1,1.9 103,7.1,3.0,5.9,2.1 104,6.3,2.9,5.6,1.8 105,6.5,3.0,5.8,2.2 106,7.6,3.0,6.6,2.1 107,4.9,2.5,4.5,1.7 108,7.3,2.9,6.3,1.8 109,6.7,2.5,5.8,1.8 110,7.2,3.6,6.1,2.5 111,6.5,3.2,5.1,2.0 112,6.4,2.7,5.3,1.9 113,6.8,3.0,5.5,2.1 114,5.7,2.5,5.0,2.0 115,5.8,2.8,5.1,2.4 116,6.4,3.2,5.3,2.3 117,6.5,3.0,5.5,1.8 118,7.7,3.8,6.7,2.2 119,7.7,2.6,6.9,2.3 120,6.0,2.2,5.0,1.5 121,6.9,3.2,5.7,2.3 122,5.6,2.8,4.9,2.0 123,7.7,2.8,6.7,2.0 124,6.3,2.7,4.9,1.8 125,6.7,3.3,5.7,2.1 126,7.2,3.2,6.0,1.8 127,6.2,2.8,4.8,1.8 128,6.1,3.0,4.9,1.8 129,6.4,2.8,5.6,2.1 130,7.2,3.0,5.8,1.6 131,7.4,2.8,6.1,1.9 132,7.9,3.8,6.4,2.0 133,6.4,2.8,5.6,2.2 134,6.3,2.8,5.1,1.5 135,6.1,2.6,5.6,1.4 136,7.7,3.0,6.1,2.3 137,6.3,3.4,5.6,2.4 138,6.4,3.1,5.5,1.8 139,6.0,3.0,4.8,1.8 140,6.9,3.1,5.4,2.1 141,6.7,3.1,5.6,2.4 142,6.9,3.1,5.1,2.3 143,5.8,2.7,5.1,1.9 144,6.8,3.2,5.9,2.3 145,6.7,3.3,5.7,2.5 146,6.7,3.0,5.2,2.3 147,6.3,2.5,5.0,1.9 148,6.5,3.0,5.2,2.0 149,6.2,3.4,5.4,2.3 150,5.9,3.0,5.1,1.8
查看全部 -
import numpy as np
from numpy.linalg import inv——(矩阵的逆)
from numpy import dot——(矩阵的点成)
from numpy import mat——(矩阵)
A=np.mat([1,1])——(1x2 的矩阵)
print('A:\n',A)
#A=np.array([1,1])——(数组)
B=mat([1:2],[3:4])——(2x2的)
print('B:\n',B)
print(''A.B:',dot(A,B))——结果是错的,因为1*2和2*2矩阵是不能想乘的
那么就需要给A矩阵转置:print('A.T:\n',A.T)
还有对矩阵B求逆:print('B的逆:\n',inv(B))
print(B[0,:1])——表示取出0行一列
print(B[:,0])——表示取出的是所有行第一列,就是第一列
print(A.reshape(2,1))——就是重新改变A矩阵的大小的,变成2*1的了;它不仅可以像转置一样还可以将3*2的变成1*6的,这是转置办不到的!
以上矩阵的基本操作:
接下来是线性回归的计算:
imort numpy as np
from numpy.linalg import inv
from numpy import dot
from numpy import mat
#计算y=2x
x=mat([1,2,3]).reshape([3,1])
y=2*x
#再计算theta=(x'x)^-1x'y
theta=dot(dot(inv(dot(x.T,x)),x.T),y)
print(theta)
接下来是梯度下降的算法:
(就是根据Y与X的关系不断的进行迭代计算)
#theta=theta-alpha*(theta*X-Y)*X——alpha在(0,1)之间取值,保证下降的梯度不会太快,是函数迅速收敛,是很重的学习内容
theta=1.
alpha=0.1
for i in range(100):
theta=theta+np.sum(alpha*(Y-dot(X,theta))*X.reshape(1,3))/3.——bp.sum()可以进行加权平均,因为X是3组数,而结果theta就是一个数,所以加权平均一下,结尾出“/3.”是除以其组数
(梯度下降是逐步逼近那个值的)
接下来完成一个复杂的线性回归l:
【
import random
def Y(X1, X2, X3):
return 0.65 * X1 + 0.70 * X2 - 0.55 * X3 + 1.95
def Produce():
filename = 'data.csv'
with open(filename, 'w') as file:
file.write('Unnamed: 0,Y,X1,X2,X3\n')
for i in range(150):
random.seed()
x1 = random.random() * 10
x2 = random.random() * 10
x3 = random.random() * 10
y = Y(x1, x2, x3)
try:
file.write(str(i)+','+ str(y)+ ',' +str(x1) + ',' + str(x2) + ',' + str(x3) + '\n')
except Exception as e:
print ('Write Error')
print (str(e))
Produce()
】
查看全部 -
inv: 矩阵求逆
dot: 矩阵点乘
mat: 二维矩阵
array: 一维数组
.T: 矩阵的转置
.reshape : 重新构置矩阵
查看全部 -
梯度下降方法(第二种代码)可以很好地解决向量方法(第一种)面对大量计算无法计算的弊端
而梯度下降更重要的是进行同步更新
所以需要一个temp来进行缓存
注意矩阵的形式可能需要变形——
reshape( )(如果出错,改成values.reshape( ))
查看全部 -
inv 逆
dot 点乘
mat 矩阵
array 数组
.T 转置
查看全部 -
测试测试测试测试测试测试测试测试测试测试测试测试测试测试测试测试测试测试测试测试
查看全部 -
测试测试测试测试测试测试测试测试测试
查看全部 -
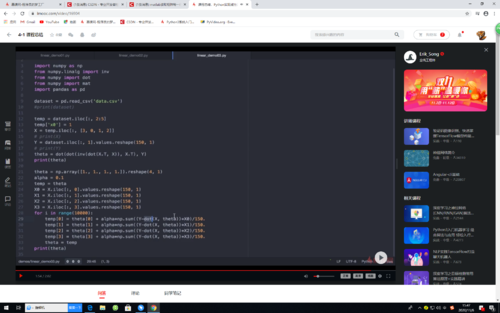
线性回归算法
矩阵算法、梯度算法
 查看全部
查看全部 -
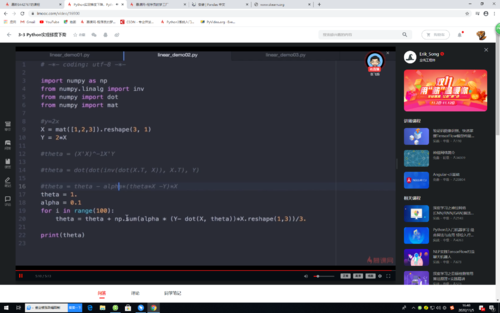
梯度下降法计算
 查看全部
查看全部 -
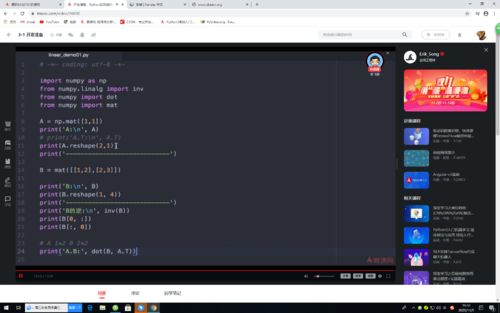
矩阵的操作
 查看全部
查看全部 -
矩阵A,B的点成:np.dot(A,B)
查看全部 -
矩阵B的逆:np.inv(B)
查看全部 -
矩阵A的转置:A.T
查看全部 -
最小二乘法模型
查看全部 -
梯度下降函数
查看全部
举报










