从入门到高阶，读懂机器学习需要哪些数学知识？

Question

从入门到高阶，读懂机器学习需要哪些数学知识

Answer 1

你必需具备的数学知识

概率论

• 离散型和连续型随机变量

• 主要分布（伯努利分布、二项式分布、正态分布、 指数分布、 泊松分布、Beta 和 Gamma 分布）

• 矩估计和最大似然估计

• 贝叶斯统计

• 相关性系数和协方差（Correlation and Covariance）

概率是机器学习算法中频繁用到的。不过基础的概率知识在统计学中已经包括了，而比较深入的概率知识其实在机器学习算法设计的时候并不经常用到。




线性代数

• 向量和矩阵

• 矩阵的行列式

• 特征向量和特征值

• 矩阵分解（如 SVD）

线性代数在深度学习领域有着举足轻重的作用，它是深度学习各种算法的基本数学工具。尤其是矩阵的各种变换，因为大量机器学习算法都是在和矩阵打交道。




向左转|向右转









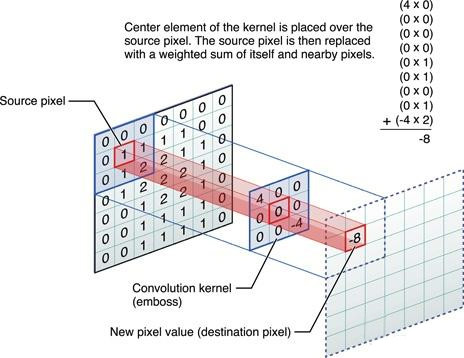
微积分

• 极限与导数

• 微分和积分

• 数值计算与最优化方法

比如，现在无比热门的神经网络，优化方法几乎全是基于梯度下降，而梯度下降，其实就是链式求导。不过，理工科应该都学过这方面的课程。




最好要掌握：

离散数学：毕竟离散数学是描述计算机问题的基础。许多算法的思想也是基于离散数学的。离散数学研究的一些问题对于描述计算机问题也有很大启发。




随机过程，实分析：机器学习往深里做肯定需要用这种，高级的数学语言去对问题进行描述。




泛函：泛函分析是一门非常抽象的课程。泛函的很多内容都是从数学分析，线性代数，实分析等抽象出来的，同时也是它们的推广，泛函研究更广泛更一般的空间，研究共性的问题。而数学分析，高等代数研究的是个性的问题，都很具体。




各种算法和理论用到的数学知识

下面我们一张图来看典型算法和理论结论所用到的数学知识：




向左转|向右转









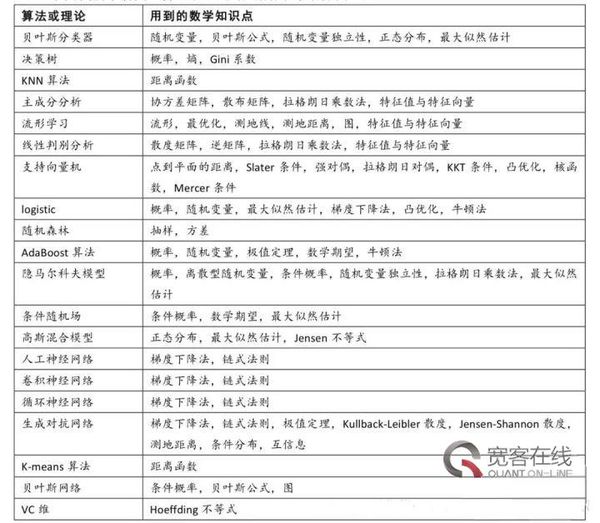
推荐书目

• 《An Introduction Statistical to Learning 》

• 《 The Elements of Statistical Learning 》

它们讲述的都是统计学习，或者机器学习的方法。其中前一本可以看成是后一本的简化版。它更通俗、更简单一些，后面这个稍微有些难。这两本书可以反复阅读，每次都有不同的收获。