Scipy Optimize CurveFit 计算错误的值

Question

我很想知道两种正弦波类型之间的相移。为此，我试图用 scipy.cuve_fit 来拟合每一波。我一直在关注这个帖子。但是，我获得了负幅度，并且相移有时看起来像转发的 pi 弧度。我正在使用的代码是下面的代码：def fit_sin_LD(t_LD, y_LD):'''Fit sin to the input time sequence, and return fitting parameters "amp", "omega", "phase", "offset", "freq", "period" and "fitfunc"'''ff = np.fft.fftfreq(len(t_LD), (t_LD[1]-t_LD[0]))   # assume uniform spacingFyy = abs(np.fft.fft(y_LD))guess_freq = abs(ff[np.argmax(Fyy[1:])+1])   # excluding the zero frequency "peak", which is related to offsetguess_amp = np.std(y_LD) * 2.**0.5guess_offset = np.mean(y_LD)guess = np.array([guess_amp, 2.*np.pi*guess_freq, 0., guess_offset])def sinfunc_LD(t_LD, A, w, p, c):    return A * np.sin(w*t_LD + p) + c#boundary=([0,-np.inf,-np.pi, 1.5],[0.8, +np.inf, np.pi, 2.5])popt, pcov = scipy.optimize.curve_fit(sinfunc_LD, t_LD, y_LD, p0=guess, maxfev=3000) # with maxfev= number I can increase the number of iterationsA, w, p, c = poptf          = w/(2.*np.pi)fitfunc_LD = lambda t_LD: A*np.sin(w*t_LD + p) + cfitted_LD  = fitfunc_LD(t_LD)dic_LD = {"amp_LD": A, "omega_LD": w, "phase_LD": p, "offset_LD": c, "freq_LD": f, "period_LD": 1./f, "fitfunc_LD": fitted_LD, "maxcov_LD": np.max(pcov), "rawres_LD": (guess, popt, pcov)}return dic_LDdef fit_sin_APD(t_APD, y_APD):''' Fit sin to the input time sequence, and return fitting parameters "amp", "omega", "phase", "offset", "freq", "period" and "fitfunc" '''ff = np.fft.fftfreq(len(t_APD), (t_APD[1]-t_APD[0]))   # assume uniform spacingFyy = abs(np.fft.fft(y_APD))guess_freq = abs(ff[np.argmax(Fyy[1:])+1])   # excluding the zero frequency "peak", which is related to offsetguess_amp = np.std(y_APD) * 2.**0.5guess_offset = np.mean(y_APD)guess = np.array([guess_amp, 2.*np.pi*guess_freq, 0., guess_offset])我不明白为什么curve_fit会返回负幅度（就物理学而言没有意义）。我也尝试将边界条件设置为 **kwargs* ：bounds=([0.0, -np.inf,-np.pi, 0.0],[+np.inf, +np.inf,-np.pi, +np.inf])但它会产生更奇怪的结果。我添加了一张显示这种差异的图片：有谁如何通过相位和幅度来克服这个问题？

Answer 1

这里有几个我不明白的问题：

1. 无需在“拟合函数”中定义拟合函数

2. 如果唯一的区别是字典的命名，则无需定义两次。（虽然我不明白为什么首先必须以不同的方式命名）

3. 一个可以直接拟合频率而不是欧米茄

4. 预先计算拟合值时，直接使用给定的fitfunction

总的来说，我不明白为什么第二次拟合会失败并且在这里使用一些通用数据，但事实并非如此。考虑到物理学中幅度可能很复杂的事实，我对负面结果没有问题。不过，我理解 OP 中的要点。当然，拟合算法不了解物理学，从数学上讲，幅度为负是没有问题的。这只是给出了 pi 的额外相移。因此，在处理所需的相移时，可以很容易地强制施加正幅度。我在这里介绍了这个作为可能的关键字参数。此外，我将其简化为一个适合函数，并可能将输出字典键“重命名”为关键字参数。

import matplotlib.pyplot as plt

import numpy as np

from scipy.optimize import curve_fit

def sinfunc( t, A, f, p, c ):

    return A * np.sin( 2.0 * np.pi * f * t + p) + c

def fit_sin(t_APD, y_APD, addName="", posamp=False):

    ''' Fit sin to the input time sequence, and return fitting parameters "amp", "omega", "phase", "offset", "freq", "period" and "fitfunc" '''

    ff = np.fft.fftfreq( len( t_APD ), t_APD[1] - t_APD[0] ) # assume uniform spacing

    Fyy = abs( np.fft.fft( y_APD ) )

    guess_freq = abs( ff[np.argmax( Fyy[1:] ) + 1] )   # excluding the zero frequency "peak", which is related to offset

    guess_amp = np.std( y_APD ) * 2.**0.5

    guess_offset = np.mean( y_APD )

    guess = np.array( [ guess_amp, guess_freq, 0., guess_offset ] )

    popt, pcov  = curve_fit(sinfunc, t_APD, y_APD, p0=guess, maxfev=500) # with maxfev= number I can increase the number of iterations

    if popt[0] < 0 and posamp:

        popt[0] = -popt[0]

        popt[2] += np.pi 

        popt[2] = popt[2] % ( 2 * np.pi )

    A, f, p, c  = popt 

    fitted_APD  = sinfunc( t_APD, *popt )

    dic_APD     = {

            "amp{}".format(addName): A, 

            "omega{}".format(addName): 2.0 * np.pi * f, 

            "phase{}".format(addName): p, 

            "offset{}".format(addName): c, 

            "freq{}".format(addName): f, 

            "period{}".format(addName): 1.0 / f, 

            "fitfunc{}".format(addName): fitted_APD, 

            "maxcov{}".format(addName): np.max( pcov ), 

            "rawres{}".format(addName): ( guess, popt, pcov ) }

    return dic_APD

tl = np.linspace(0,1e-6, 150 )

sl1 = np.fromiter( (sinfunc(t, .18, 4998735, 3.6, 2.0 ) + .01 *( 1 - 2 * np.random.random() ) for t in tl ), np.float )

sl2 = np.fromiter( (sinfunc(t, .06, 4998735, 2.1, 0.4 ) + .01 *( 1 - 2 * np.random.random() ) for t in tl ), np.float )

ld = fit_sin(tl, sl1, addName="_ld" )

print ld["amp_ld"]

ld = fit_sin(tl, sl1, addName="_ld", posamp=True )

print ld["amp_ld"]

apd = fit_sin(tl, sl2 )

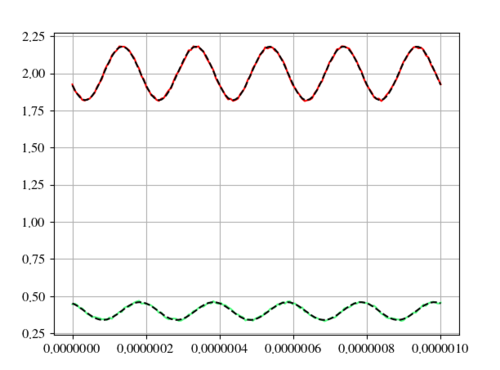
fig = plt.figure("1")

ax = fig.add_subplot( 1, 1, 1 )

ax.plot( tl, sl1, color="r" )

ax.plot( tl, ld["fitfunc_ld"], color="k", ls="--" )

ax.plot( tl, sl2, color="#50FF80" )

ax.plot( tl, apd["fitfunc"], color="k", ls="--" )

ax.grid()

plt.show()

这给了我：

-0.180108427200549

0.180108427200549

即在第一次尝试中，尽管对幅度进行了很好的猜测，但结果为负。这可能是由于大相位。由于该猜测为零，因此算法更容易先切换幅度的符号，然后再调整相位。如上所述，这很容易纠正，甚至不需要错误传播。