将模型函数拟合到定义的数据范围

Question

假设我有一组(x=times,y=observation)有多个时间间隔的数据。无论数据趋势是什么，我们都假设它是线性的。在时间间隔内，有一个衰减，使数据偏离纯线性趋势，直到再次开始观察并恢复线性趋势。时间上有多个间隔，但在这个例子中，我只报告了最短的快照来说明问题。时间间隔是（正）线性趋势之间没有可用观察值的时间，因此连续之间的差异x=times（远）大于平均值。我想将衰减建模为函数 ( y_decay = C -D*x)的一部分from scipy.optimize import curve_fitimport matplotlib.pyplot as pltdef f(x, A, B, C, D):    line = A*x + B if ((x>=1) & (x<=3) | (x>=5) & (x<=9) | (x>=23) & (x<=25)) else C-D*x    return linex=[1,2,3, 12,13,14, 23,24,25]y=[2,4,6, 5, 7, 9, 8, 10,12]popt, pcov = curve_fit(f, x, y) figure = plt.figure(figsize=(5.15, 5.15))figure.clf()plot = plt.subplot(111)ax1 = plt.gca()plot.scatter(x,y)plt.show()如何将decay变量建模为函数的一部分并获得其最佳拟合值？

Answer 1

在完全周期性的情况下，我会做这样的事情：

import matplotlib.pyplot as plt

import numpy as np

from scipy.optimize import leastsq

def data_func( x, x0, a, bc, off, p1, p2):

    """

    fit function that uses modulus to get periodicity

    two linear functions are combines piecewise by boxing them

    using the heaviside function with the periodic input

    over all slope is added.

    Note that the "decay" part maybe positive with this solution.

    """

    P1 = abs(p1)

    P2 = abs(p2)

    X = x - x0

    P= P1 + P2

    mod = X % P

    y0 = a * P1

    beta = y0 * P / P2

    slope = y0 / P2

    box1 =  np.heaviside( +np.abs( ( X - P1 / 2. ) % P - 0.5 * P ) - 0.5 * P2, .5 )

    box2 =  np.heaviside( -np.abs( ( X - P1 / 2. ) % P - 0.5 * P ) + 0.5 * P2, .5 )

    out = a * mod * box1 

    out += (beta - slope * mod  )* box2

    out += off + bc * X

    return out

def residuals( params, xl ,yl ):

    x0, a, bc, off, p1, p2 = params

    diff = np.fromiter( ( y - data_func( x, x0, a, bc, off, p1, p2 ) for x, y in zip( xl, yl )  ), np.float )

    return diff

theOff = 0.7

theP1= 1.8869

theP2 = 5.21163

theP = theP1 + theP2

xdata = np.linspace(-1, 26, 51 )

xdata = np.fromiter( ( x for x in xdata if (x-theOff)%theP <= theP1 ),np.float )

ydata = np.fromiter( ( data_func( x, theOff, .6, .1, 17, theP1, theP2) for x in xdata ),np.float )

tl = np.linspace(-1, 26, 150 )

yl = np.fromiter( ( data_func( x, theOff, .6, .1, 17, theP1, theP2) for x in tl ),np.float )

guess= [0, 0.55, .1, 16 , 2, 5 ]

sol, err = leastsq( residuals, guess, args = ( xdata, ydata ) )

print sol

### getting the real slopes out of the data

s1 = sol[1]+ sol[2] 

s2 =  - sol[1] * sol[4] / sol[5] + sol[2]

print "real slope1 = {}".format( s1 )

print "real slope2 = {}".format( s2 )

fit = np.fromiter( ( data_func( x, *sol ) for x in tl ),np.float )

fig = plt.figure()

ax = fig.add_subplot( 1, 1, 1 )

### original data

ax.plot( tl, yl, ls='--')

ax.plot( xdata, ydata, ls='', marker='+')

### fit

ax.plot( tl, fit )

### check the slopes

short = np.linspace(0, 3, 3)

ax.plot( short, [ 17 + s1 * s for s in short ] )

short = np.linspace(3, 10, 3)

ax.plot( short, [ 18 + s2 * s for s in short ] )

ax.grid()

plt.show()

这使：

>> [ 0.39352332  0.59149625  0.10850375 16.78546632  1.85009228  5.35049099]

>> real slope1 = 0.7

>> real slope2 = -0.0960237685357

和

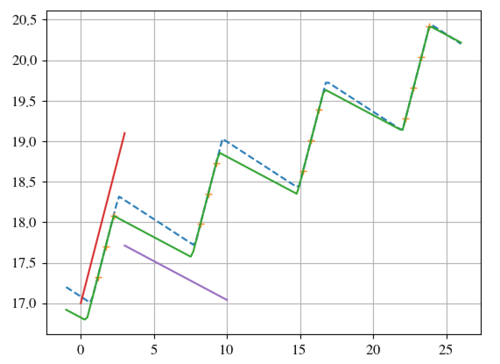
自然地，间隙中缺乏信息会导致那里的斜率相当糟糕。结果，在周期性中存在相应的误差。如果知道这一点，那么准确度当然会提高。

您需要对起始参数进行合理的猜测！

Answer 2

当假设所有数据都具有相同的斜率m并且所有“衰减”斜率时，那将是我的 AnsatzD

import matplotlib.pyplot as plt ### only for plotting; not important for the OP

import numpy as np ### for easy data manipulation

from scipy.optimize import leastsq ### one of many possibilities for optimization

def generic_data( m, D, n ): ### just generating data; not important for OP

    alpha0 = 0

    timel = [ 0 ] ### to avoid errer, remove at the end

    dl = list()

    for gaps in range( n + 1 ): 

        for pnts in range( 3 + np.random.randint( 2 ) ): 

            timel.append ( timel[-1] +  0.5 + np.random.rand() )

            dl.append( m * timel[ -1 ] + alpha0 )

        ###now the gap

        dt =  2. + 2 * np.random.rand()

        timel.append ( timel[-1] + dt )

        dl.append( dl[-1] - D * dt )

        alpha0 = dl[-1] - m * timel[-1]

    del timel[0]

    ### remove jump of last gap

    del timel[-1]

    del dl[-1]

    dl = np.fromiter( ( y + np.random.normal( scale=0.1 ) for y in dl ), np.float )

    return np.array( timel ), dl

def split_into_blocks( tl, dl ):

    """

    identifying the data blocks by detecting positions of negative slope.

    first subtract a shifted version of the data from itself

    find the negatives and get their positions

    get sub-lists based on this positins 

    """

    mask = np.where( dl[1::] - dl[:-1:] < 0, 1, 0 )

    where = np.argwhere( mask )

    where = where.reshape( 1, len( where ) )[0]

    where = np.append( where, len( dl ) - 1 )

    where = np.insert( where, 0, -1 )

    tll = list()

    dll = list()

    for s, e in zip( where[ :-1:], where[ 1:: ] ):

        dll.append( dl[ s + 1 : e + 1 ] )

        tll.append( tl[ s + 1 : e + 1 ] )

    return np.array( tll ), np.array( dll )

def residuals( params, tblocks, dblocks ):

    """

    typical residual function to be called by leastsq

    """

    ### split parameters

    nob = len( tblocks )

    m = params[0] ### all data with same slope

    D = params[1] ### all decay with same slope

    alphal = params[2:2+nob] ### off sets differ

    betal = params[-nob+1::]

    out = list()

    ### evaluate diefference between data and test function

    for i, (tl, dl) in enumerate( zip(tblocks, dblocks ) ):

        diff = [ d - ( m * t + alphal[i] ) for t, d in zip( tl, dl ) ]

        out= out + diff

    ### evaluate differences for the gapfunction; this could be done

    ### completely independent, but I do it here to have all in one shot.

    for j in range( nob -1 ):

        out.append( dblocks[ j][-1] - ( betal[j] + D * tblocks[j][-1] ) ) ###left point gap

        out.append( dblocks[ j+1][0] - ( betal[j] + D * tblocks[j+1][0] ) ) ###right point gap

    return out

### create generic data

tl, dl =  generic_data( 1.3, .3, 3 )

tll, dll = split_into_blocks( tl, dl )

### and fit

nob = len(dll)

m0 = +1.0

D0 = -0.1

guess = [m0, D0 ]+ nob * [-3] + ( nob - 1 ) * [ +4 ]

sol, err = leastsq( residuals, x0=guess, args=( tll, dll ) )

mf = sol[0]

Df = sol[1]

print mf, Df

alphal = sol[2:2+nob]

betal = sol[-nob+1::]

### ... and plot

fig = plt.figure()

ax = fig.add_subplot( 1, 1, 1 )

###original data

ax.plot( tl, dl, ls='', marker='o')

###identify blocks

for a,b in zip( tll, dll ):

    ax.plot( a, b, ls='', marker='x')

###fit results

for j in range(nob):

    tloc = np.linspace( tll[j][0] - 0.3, tll[j][-1] + 0.3 , 3 )

    ax.plot( tloc, [ mf * t + alphal[j] for t in tloc ] )

for j in range(nob - 1):

    tloc = np.linspace( tll[j][-1] - 0.3, tll[j+1][0] + 0.3 , 3 )

    ax.plot( tloc, [ Df * t +betal[j] for t in tloc ] )

plt.show()

这导致

>> 1.2864142170851447 -0.2818180721270913

和

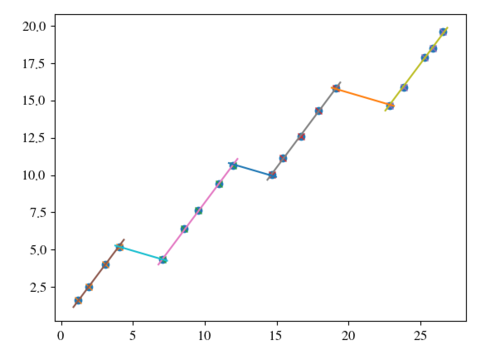
然而，该模型可能要求衰减线不与数据范围内的数据线相交。这使得额外的摆弄成为必要，因为我们需要检查某种类型的边界。另一方面，可以只拟合数据并寻找具有满足前面提到的边界的最小可能斜率的衰减曲线。因此，在这种情况下，我会D从残差中删除拟合部分，然后再计算它。