如何去除数据中的移动平均线？

Question

我有数据 y = [-10.5, -2.0, 5.0, -3.0, 4.0, 9.5, 18.0, 14.5, 11.0, 13.5, 25.0, 21.5, 7.5, 5.5, 3.5, 10.5, 7.0, 3.5, 1.5, 16.0, 20.0, 22.5, 20.5, 33.5, 27.0, 38.5, 29.0, 27.0, 28.0, 24.5, 24.0, 29.5, 39.5]我想摆脱垂直移动平均线趋势（只获得围绕恒定平均值的差异）。在这种情况下，我应该得到类似的东西：[-7, -2, 2, -4, 0, 3, 8, 5, 2, 3, 10, 7, -3, -5, -7, -3, - 6, -9, -11, -2, 0, 1, -1, 7, 2, 9, 2, 0, 0, -3, -4, -1, 5]输入 输出我的想法是在Input上拟合一条线（线性回归），得到类似 ax + b 的东西并仅删除 ax 以近似所需的Output。有没有更标准的数学方法来解决我的问题？（最好用 Python 实现）。另外，我认为Output和 mean( Output )的不同值之间的一些差异可能被错误地视为直线斜率的一部分，因此，线性回归可能会给我一个 a'x + b'，其中 a' 关闭但不同于 a. 我怎样才能缓解这个问题？

Answer 1

考虑到疯狂的 FFT 优化，我认为 1D 卷积会很快完成你想要的事情：

import numpy as np

from scipy.signal import convolve

window_size = 10

y = np.array([-10.5, -2.0, 5.0, -3.0, 4.0, 9.5, 18.0, 14.5, 11.0, 13.5, 25.0, 21.5, 7.5, 5.5, 3.5, 10.5, 7.0, 3.5, 1.5, 16.0, 20.0, 22.5, 20.5, 33.5, 27.0, 38.5, 29.0, 27.0, 28.0, 24.5, 24.0, 29.5, 39.5])

# Pad with zeros for entries before/after the window size

y_rolling_mean = convolve(y, np.ones(window_size)/window_size, 'same')

y_without_mean = y - y_rolling_mean

请记住，这通常会为第一个和最后一个 window_size//2 条目产生不准确的值，因为它们的滚动平均值是使用零填充计算的，但是您可以通过在卷积之前填充您想要的值来更改此行为。

更新：添加了一个图来与第二个答案进行比较

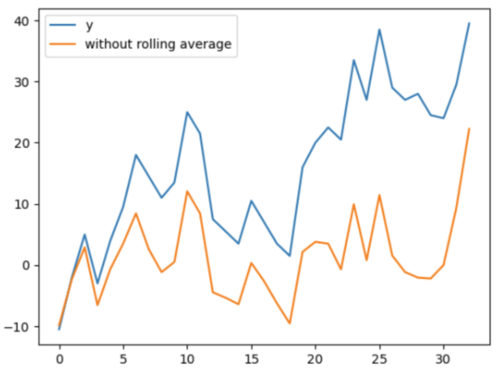
卷积如何找到滚动平均值？

本质上，一维卷积可以被认为是两个数组的点积，因为一个数组“滑动”到另一个数组（实际上，相关性在技术上对于这种情况是正确的，但我现在不会深入讨论）。为了获得更好的想法，请考虑以下场景：

y = 1 2 3 4 5 6

x = 1 1 1

c = <convolution of y and x>

卷积数组的每个输出索引都是“x”与其相同长度窗口与 y 的点积。所以

c[0] = sum(y[0:3]*x)

c[1] = sum(y[1:4]*x)

c[2] = sum(y[2:5]*x)

...

现在，考虑 N 个数字的平均值就是 sum(numbers)/N 这一事实。或者：

mean = sum(1/N * number)

结合我们在上面学到的关于卷积的知识，让 x = 1/len(x) 的每个元素：

y =  1    2    3   4  5   6

x = 1/3  1/3  1/3

c[0] = 1/3*y[0] + 1/3*y[1] + 1/3*y[2] = mean(y[0:3])

c[1] = 1/3*y[1] + 1/3*y[2] + 1/3*y[3] = mean(y[1:4]

...

整洁的！与特殊形式的 x 向量卷积的副作用是该范围的平均值！因此，通过将 x 选择为 be，np.ones(window_size)/window_size您可以保证卷积将在 上产生滚动平均值y。

当图像中存在大量不需要的高频噪声时，这在图像处理中大量使用：

请注意，与您的一维数据类似，噪声图像中的尖锐“峰”和斑点被“舍入”了。

为什么窗口大小为 10？

老实说，我随机选择了窗口大小。实际上，这在很大程度上取决于您期望数据的噪声程度以及您希望输出看起来有多“平滑”。窗口大小越大，输出看起来越平坦。根据提供的玩具编号，似乎有一个 10 的窗口可以在y不破坏信号的情况下压平足够的尖峰。

Answer 2

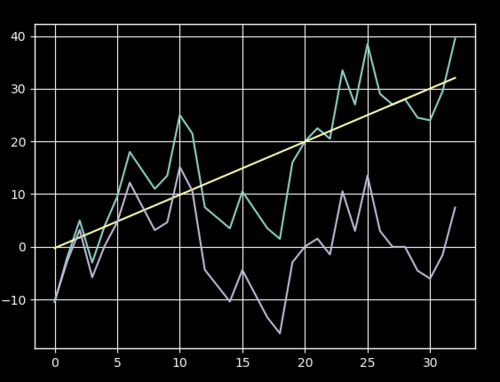
正如您在问题中提到的线性拟合的想法，我会寻求简单但相当稳健的解决方案，即拟合最佳线并简单地从数据中减去它以获得去趋势跟踪：

import numpy as np

import matplotlib.pyplot as plt

x = np.arange(len(y)) 

coefs = np.polyfit(x, y, 1)

line = coefs[1] + x*coefs[0]

detrended = y-line

fig, ax = plt.subplots(1)

ax.plot(y)

ax.plot(line)

ax.plot(detrended)