-
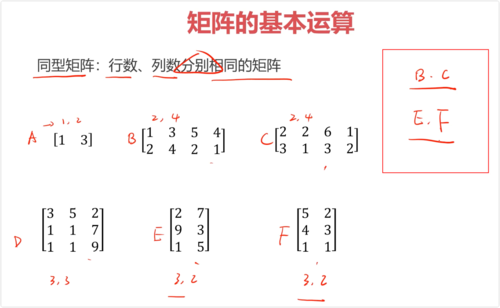
同型矩阵:行数、列数分别相同的矩阵
必须是同型号矩阵才能进行加减运算
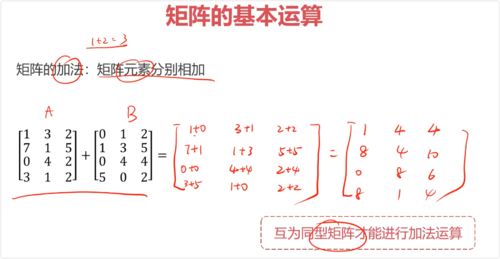
加法:矩阵元素分别相加,满足交换律、结合律
减法:矩阵元素分别相减
负矩阵:矩阵元素互为相反数关系的矩阵(负矩阵必定为同型矩阵)(矩阵前面有 - 负号)

矩阵的加法:矩阵元素分别相加(互为同型矩阵才能进行加法运算)
矩阵的加法满足交换律、结合律,即:
A+B=B+A
A+B+C=A+(B+C)
矩阵的减法可以理解为对负矩阵的加法,即:
A-B=A+(-B)

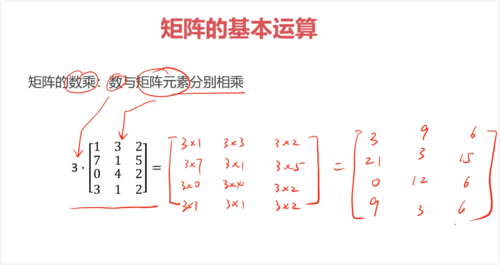
矩阵的数乘:数与矩阵元素分别相乘
矩阵的数乘满足交换律、结合律、分配律

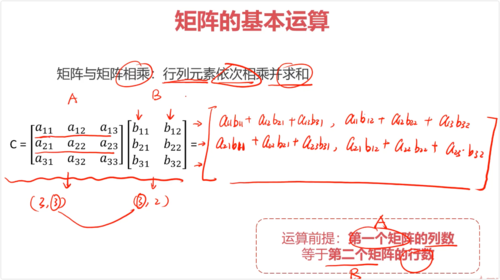
矩阵与矩阵相乘:行列元素依次相乘并求和(第一个矩阵列数等于第二个矩阵行数)
矩阵与矩阵相乘不满足交换律,但满足结合律、分配律
 查看全部
查看全部 -
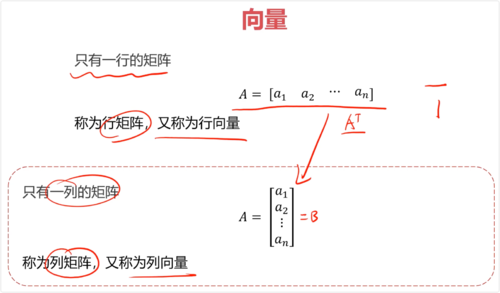
一、向量
行向量:只有一行的矩阵
列向量:只有一列的矩阵,行向量的转置
二、向量的基本运算
遵循矩阵基本运算规则
矩阵与向量相乘,结果仍为向量
 查看全部
查看全部 -
# python的矩阵运算 import numpy as np A = np.array([[1,2,3],[6,6,6],[7,8,9]]) print(A)
查看全部 -
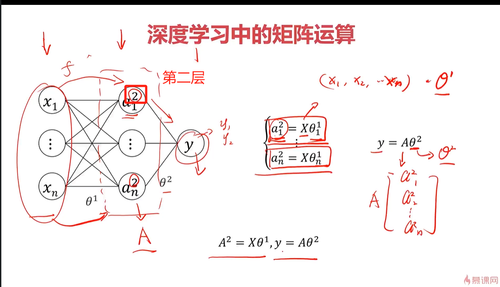
深度学习可以理解为层层递进的关系
中间层A=元素X*系数+常数
输出值Y=中间层A*系数+常数
多层次则逐层运算
查看全部 -
积分公式计算公式计算
 查看全部
查看全部 -
积分公式计算公式计算
 查看全部
查看全部 -
 概率分析查看全部
概率分析查看全部 -

学习大纲总结
查看全部 -
一、实战 - 朴素贝叶斯的使用
调用sklearn 朴素贝叶斯模块CategoricalNB, 训练模型基于用户基本信息,预测其购买商品的概率。
import pandas as pd import numpy as np # 数据加载 data = pd.read_csv("data.csv") data.head() # X赋值 X = data.drop(['y'], axis = 1) # y 赋值 y = data.loc[:, 'y'] # 建立模型 # pip install sklearn from sklearn.native_bayes import CategoricalNB # 建立模型实例 model = CategoricalNB() # 模型训练 model.fit(X, y) y_predict_prob = model.predict_proba(X) # 输出预测y y_predict = model.predict(X) # 计算模型准确率 from sklearn.metrics import accuracy_score accuracy = accuracy_score(y, y_predict) # 测试样本的预测 X_test = np.array([0,0,0,1,1,0]) y_test_proba = model.predict_proba(X_test) y_test = model.predict(X_test)查看全部 -
一、贝叶斯公式
在已知一些条件下(部分事件发生的概率),实现对目标事件发生概率更准确的预测
P(B|A) = P(B) * P(A|B) / P(A)
贝叶斯公式则是利用条件概率和全概率公式计算后验概率
二、朴素贝叶斯
以贝叶斯定理为基础,假设特征之间相互独立,先通过训练数据集,学习从输入到输出的概率分布,再基于学习到的模型及输入,求出使得后验概率最大的输出实现分类。
P(Y|X) = P(Y) * P(X|Y) / P(X)
查看全部 -
一、条件概率与全概率
条件概率:事件A已经发生的条件下事件B发生的概率 P(B|A)
P(B|A) = P(AB) / P(A) # P(AB) AB同时发生的概率
全概率:将复杂事件A的概率求解问题,转化为在不同情况下发生的简单事件的概率的求和问题
查看全部 -
一、概率基础知识
矩阵、微积分 ---> 回归;概率 ---> 分类
概率:可能性的度量 likehood
查看全部 -
一、Python 实现微分与积分
使用 sympy 包
import sympy as sp
x = sp.Symbol('x')
y = 3 * x ** 2 # ** 幂运算
# 求导(求微分)
f1 = sp.diff(y)
# 求积分
F1 = sp.integrate(f1, x)
# 求极限
x = 0 时
L1 = sp.limit(y1, x, 0)
查看全部 -
一、积分
逆运算:导数推出原函数 --> 积分
不定积分:函数f的不定积分,是一个可导函数F且其导数等于原来的函数f
定积分:对于一个给定的正实数函数f(x),在一个实数区间上的定积分可以理解为在坐标平面上,由曲线、直线以及轴围成的曲边梯形的面积值。
作用:求面积,确定概率

查看全部 -
一、梯度下降法 (梯度即导数)
寻找极小值的一种方法。通过向函数上当前点对应梯度(导数)的反方向的规定步长距离点进行迭代搜索,直到在极小点收敛。
核心:从一个点出发,沿着导数的反方向逐步逼近极值点。
查看全部
举报







