-
朴素贝叶斯查看全部 -
贝叶斯公式延申查看全部 -
贝叶斯公式查看全部 -
全概率查看全部 -
全概率公式查看全部 -
全概率公式查看全部 -
条件概率查看全部 -
常用积分公式查看全部 -
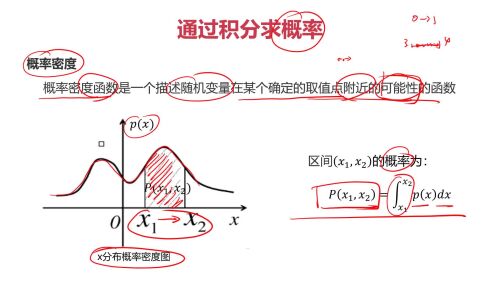通过积分求概率查看全部 -
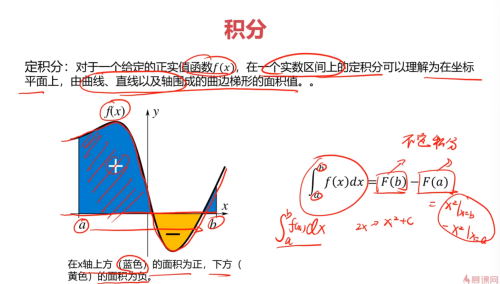定积分查看全部 -
不定积分查看全部 -
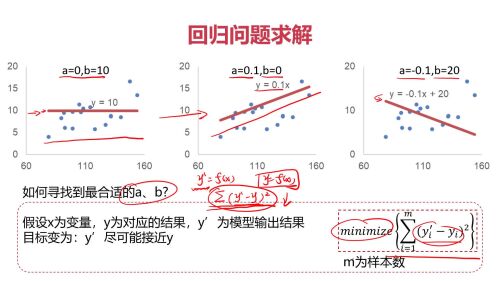回归问题求解查看全部 -
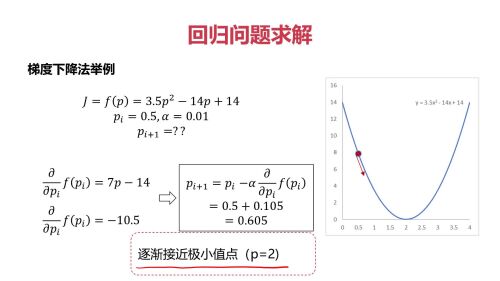回归问题求解查看全部 -
梯度下降法查看全部 -
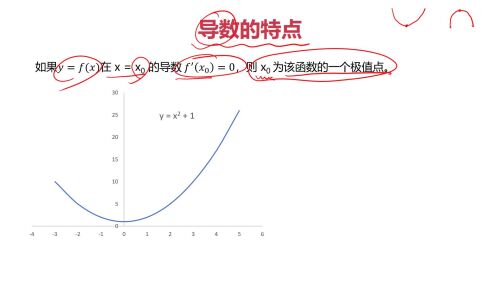导数特点查看全部 -
常用导数公式查看全部 -
学习资料链接；链接2为免费：
查看全部 -
求一个函数的极值就是求解函数的导数为零的时候的 x的值。
查看全部 -
求解导数的目的是在一些模型中需要求解一个损失函数的最小值，这个时候的方法就是求解一个函数的导数，来求得损失函数的最小值。这个是导数在 AI 中的意义。
查看全部 -
1
查看全部 -
1查看全部 -
1查看全部 -
向量
行矩阵、行向量: 只有一行的矩阵
列矩阵、列向量: 只有一列的矩阵
满足矩阵基本运算原则。
矩阵与向量相乘，结果仍为向量。
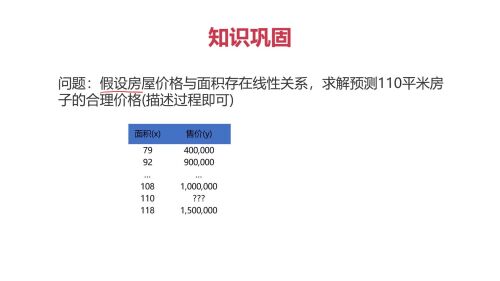查看全部 -
同型矩阵：行列相同
负矩阵：元素互为相反数
加法/减法(同型矩阵)：相同位置数相加/相减
数乘：单个数字和矩阵相乘，单个数字和矩阵每个数字相乘
矩阵和矩阵相乘：行列元素依次相乘并求和。
第一个矩阵的列数要求等于第二个矩阵的行数
不满足交换律,满足结合律和分配律
查看全部 -
同型矩阵：行数、列数分别相同的矩阵
比如两个3x2的矩阵A和B，那它们两个就是同型矩阵
负矩阵：矩阵元素互为相反数关系的矩阵
矩阵的负矩阵必然是它的同型矩阵
互为同型矩阵才能进行加减法运算
矩阵的加法满足交换律、结合律：
A + B = B + A
A + B + C = A + (B + C)
数乘：数与矩阵元素分别相乘
矩阵的数乘满足交换律、结合律、分配律，假设λ和μ是两个数字：
λA = Aλ
λAμ = λ(Aμ)
λ(A + B) = λA + λB
矩阵乘法不满足交换律，满足结合律、分配律：
AB ≠ BA
(AB)C = A(BC)
A(B + C) = AB + AC
查看全部 -
一、条件概率与全概率条件概率：事件A已经发生的条件下事件B发生的概率 P(B|A)
P(B|A) = P(AB) / P(A)
P(AB) AB同时发生的概率
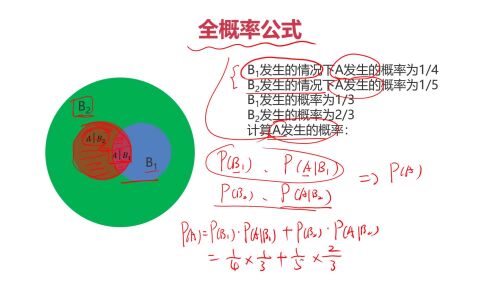
全概率：将复杂事件A的概率求解问题，转化为在不同情况下发生的简单事件的概率的求和问题
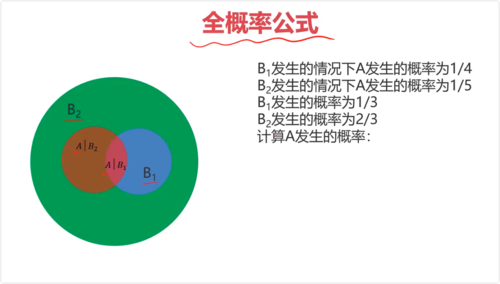
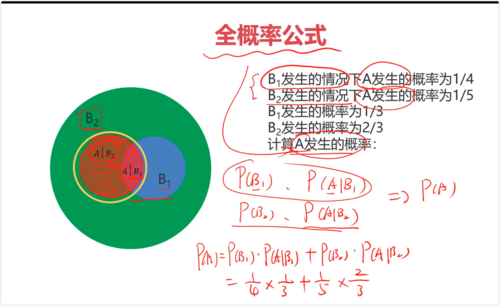
A 的概率就是 用橙黄色标记的圆环内的圆。
全概率公式是概率论中的一个重要公式，它用于计算一个事件的概率，当这个事件可以通过几个互斥的途径发生时。具体来说，如果我们有一个样本空间 SS 和一个事件 AA，并且样本空间可以被划分为几个互斥的事件 B1,B2,...,BnB1,B2,...,Bn（即这些事件两两不相交，并且它们的并集是整个样本空间），那么事件 AA 的概率可以表示为：
P(A)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+...+P(A∣Bn)P(Bn)P(A)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+...+P(A∣Bn)P(Bn)
其中：
P(A)P(A) 是事件 AA 发生的概率。
P(A∣Bi)P(A∣Bi) 是在事件 BiBi 发生的条件下事件 AA 发生的条件概率。
P(Bi)P(Bi) 是事件 BiBi 发生的概率。
全概率公式的直观理解是：要计算事件 AA 的总概率，我们可以分别计算在每个互斥事件 BiBi 发生的情况下 AA 发生的概率，并将这些概率加权求和，权重就是每个 BiBi 发生的概率。
这个公式在实际应用中非常有用，特别是在处理复杂问题时，可以通过分解问题来简化计算
查看全部 -
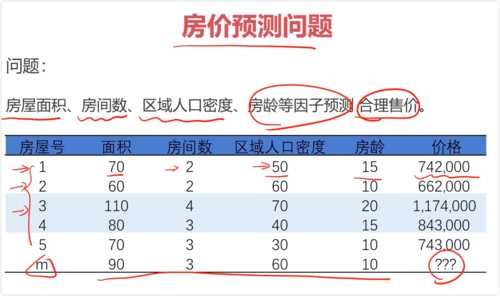
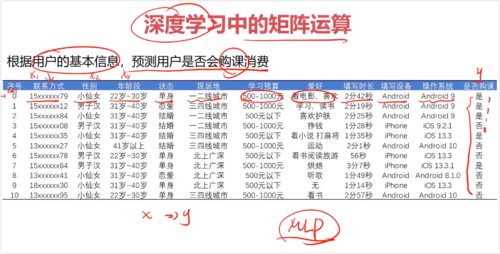
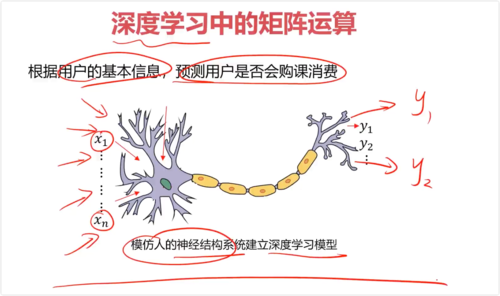
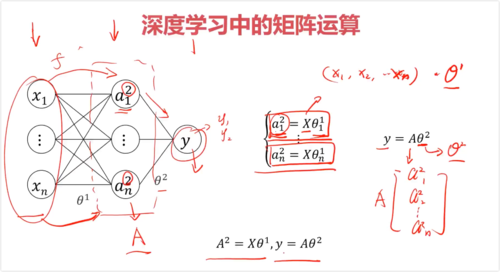
一、机器学习中的矩阵运算
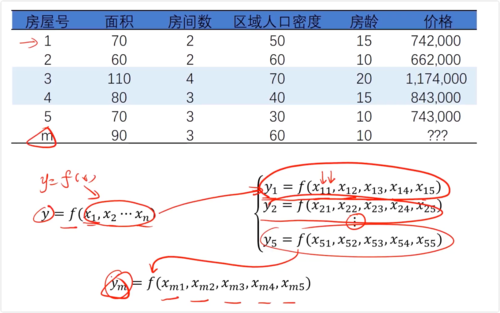
函数关系：y = f(x1, x2, x3, ...)
y = Ax + B, 求A，B
x为矩阵，系数θ为列向量
y = [x][θ] + b
查看全部
举报